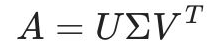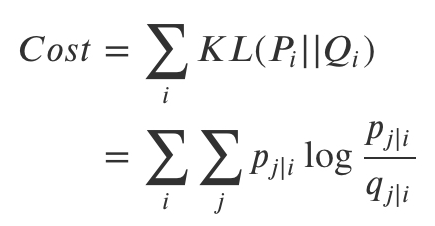NLP 시작부터 전문가까지

형태소 분석기에서 주의해야 할 점이 있다. ​ 만약 우리가 '가우스전자' 라는 기업의 데이터 분석 팀에 속해있다면 우리는 가우스전자라는 토큰은 섬세히 처리해야 한다. ​ 그 이유를 보여주겠다. >>> from konlpy.tag import Mecab >>> tokenizer =Mecab() >>> tokenizer.morphs("가우스전자 텔레비전 정말 좋네요") ['가우스', '전자', '텔레비전', '정말', '좋', '네요'] KoNLPy에서 은전한닢을 이용하여 형태소분석을 하였지만 가우스전자를 가우스,전자 로 나뉘어서 분석해버린다. ==> 단어 임베딩 품질이 떨어진다. ​ 그래서 우리는 '가우스전자' 라는 단어를 사용자 사전에 추가해서 강제적으로 하나의 토큰으로 분석될 수 있도록 할 수 있다. ..

참고자료 - https://fish-tank.tistory.com/103 ​ colab 에서 작업해보았다. ​ !git clone https://github.com/kakao/khaiii.git !pip install cmake ​ !mkdir build !cd build && cmake /content/khaiii !cd /content/build/ && make all !cd /content/build/ && make resource !cd /content/build && make install !cd /content/build && make package_python !pip install /content/build/package_python 다음을 통해 kahiii를 다운받는다 ​ ​ 이후 fro..

KoNLPy (코에넬파이) : 은전한닢,꼬꼬마,한나눔,Okt,코모란과 같은 오픈소스 형태소분석기를 파이썬 환경에서 사용가능하게 인터페이스를 통일하여 만든 한국어 자연어 처리 패키지이다. ​ ​ 1. '한국어 임베딩' 저자의 Docker image를 다운받아 컨테이너를 실행한후 파이썬 환경에 접근한다. ​ (colab에서도 가능하고 그에 대한 설명은 다음 사이트에 나와있다. https://colab.research.google.com/drive/1MWlm6-2sW_zfQMxr1Bt9A5ggvcjBF_e6?usp=sharing#scrollTo=uKkTCajXih1u) 한국어 임베딩 - 실습 https://colab.research.google.com/drive/1MWlm6-2sW_zfQMxr1Bt9A5ggv..

특이값 분해를 이해하기 위해서는 행렬에 대한 기초지식이 필요하다. ​ 다음 링크에서 자세한 이해가 가능하다. https://angeloyeo.github.io/2019/08/01/SVD.html#fn:1 ​ ​ 간단하게 말하자면, 1. 행렬분해를 통해 하나의 원본을 여러개로 쪼개어 표현할 수 있다. 2. 쪼개어진 여러개의 정보들 중에 중요한 정보들 몇개만을 선택한다. 3. 그들의 합만으로도 원본에 가까운 결과를 구현할 수 있다 4. 이때 행과 열중 차원 축소하고 싶은 부분을 찾아 그 구분에 맞게 축소된 U를 쓰던지, 축소된 VT를 쓰는지를 정해 차원을 낮추는 것(차원축소)가 가능하다는 것이다. ​ ​ 원본(=높은차원) ⇒ 다시 짜맞춘 결과물(낮은차원) ​ 자세히 말하자면, 행렬 분해 각 행렬의 성질 ​ ..

1. 한국어 임베딩(이기창 저) : 개념, 이론 2. 텐서플로2와 머신러닝으로 시작하는 자연어처리 (전찬욱,최태균,조중현,신성진 저) : 코드 중심 제 포스트는 기본적으로 1. 한국어 임베딩으로 시작할 것이고, 이후에 2 로 넘어가서 코드까지 정리하려 합니다.

고차원 데이터를 보기 쉬운 저차원으로 시각화하는 기법 → https://ratsgo.github.io/machine learning/2017/04/28/tSNE/ (책 작가의 블로그) ​ ​ 위를 간단히 정리하면 차원축소의 목적 : 각 데이터간의 거리관계를 저차원에서도 잘 표현하기 > ​ ⇒ SNE란? ​ 1. 고차원에서의 데이터간의 관계를 확률로 표현 : p 저차원에서의 데이터간의 관계를 확률로 표현 : q 즉, p와 q가 유사할수록 차원축소가 잘 되었다고 볼수 있다. 이를 수학적으로 계산하기 위해 다음 식을 이용한다. Cost 식 ​ p와q가 유사할수록 Cost가 작아진다.(p와q가 유사하면 1이되고 로그1은 0이기 때문) ​ ​ 2. 이제 Cost가 작을수록 p와q가 유사하고 p와q가 유사하다는 것..

nlp에 대한 블로그 포스트를 하려 합니다. 누구나 이해할 수 있는 설명을 적어놓는 것이 목표입니다. 초보부터 시작할 수 있도록 어느정도 포스트가 정리가 되면 커리큘럼을 적어 놓겠습니다. 감사합니다. 제 네이버 블로그 주소는 : https://blog.naver.com/gypsi12 입니다.