
트랜스포머라고 하면 위의 로봇영화가 가장 먼저 떠오를 것이다.
논문 저자가 모델 이름을 트랜스포머라고 지은 이유가 무엇일까?
영어로 transform을 검색해보면

다음과 같고, transformer는 변형시키는 것으로써 변압기를 나타내는 말이기도 하다.
하지만 이런 생명력이 없는 시시한 의미보다는 저 두번째, 완전히 바꿔 놓는다는 의미가 눈에 띤다.
실제로 Transformer는 NLP분야를 완전히 뒤흔들어 놓았다.
목차
1. 기본적인 모델 이해
2. 자세한 논문 리뷰
참고한 사이트는 다음과 같고, 이미지 또한 이 사이트에서 가져왔다.

가장 간단한 번역기 모델로 transformer를 이해를 해보자.

논문에서 자세히 표현한 그림은 다음과 같고

가장 간단히 요약하자면 다음과 같을 것이다.

INPUT을 집어넣지만 ENCODERS와 DECODERS를 거친다. 여러개의 인코더와 디코더를 사용한다는 소리이다.
흐림이 보이도록 그린다면

다음과 같이 하위 인코더의 출력이 상위 인코더의 입력으로 들어가는 것을 볼 수 있다.
또한 인코더와 디코더의 개수가 같다는 것도 알 수 있다.
하지만 논문에서 인코더를 6개를 쌓은 것에 대한 논리적 근거는 없고, 작업에 맞게 조정하면 된다.
인코더와 디코더를 여러개 쌓은 이유를 생각해 보자면, 매개변수의 개수를 늘려주기 위함으로 보인다.
그렇다면 인코더 내부는 어떻게 생겼을까? 이전 Seq2seq처럼 RNN,LSTM,GRU를 사용했을까?
아니다.
이전에는 Attention을 통해 얻은 벡터를 RNN셀의 은닉 상태와 더해서 성능을 향상하는 도구로 썻다면,
Transformer에서는 Attention만을 사용해 인코더셀을 만들었다.
게다가 성능까지 더 잘나왔다.
(Attention에 대한 이해)
하지만, 의문이 들 수 있다.
RNN은 입력 순서 정보를 전달하는 것이 가능하다. 그렇기 때문에 단어의 배치 순서가 중요한 nlp에서 사용했다.
Attention은 단어간 유사도 정보를 담은 벡터를 만들어 낼 뿐, 순서 정보(시간에 따른 정보)를 담지 못하는 것이 아닌가?
그래서, 이를 보완해주기 위해 따로 positional encoding이란 단계를 추가했다.

Embedding 벡터와 positional encoding 벡터를 더하여 위치정보를 함유한 임베딩 벡터를 만든다.
이렇게 변환된 정보를 인코더의 입력으로 집어넣는다.
저 positional encodiing 벡터를 살펴보자면

가로축이 임베딩 단어의 차원, 세로축이 포지션 정보를 나타낸다.
포지션 별 다른 패턴을 가짐으로써 단어의 순서정보를 담는 것이 가능해진다.
이제 한개의 인코더 내부가 어떻게 생겼는지 살펴보자.

위치정보가 포함된 임베딩 벡터가 입력으로 들어가 처음으로 Self-Attention 셀을 만난다.
이때 Self-Attention 벡터가 가지는 정보가 무엇일까?
Self-Attention을 한다는 것은
입력으로 들어온 단어들이 서로서로 얼마나 유사한지를 벡터로 표현하겠다는 말이다.
1, 2, 3 이 입력으로 들어왔다면 (코사인 유사도 : 내적을 이용해),
1에 대하여 1, 2, 3이 얼마나 유사한가? => [ 1 vs 1 , 1 vs 2 , 1 vs 3] 3차원 벡터 생성됨
2에 대하여 1, 2, 3이 얼마나 유사한가? => [ 2 vs 1 , 2 vs 2 , 2 vs 3] 3차원 벡터 생성됨
3에 대하여 1, 2, 3이 얼마나 유사한가? => [ 3 vs 1 , 3 vs 2 , 3 vs 3] 3차원 벡터 생성됨
위와 같이 결과가 나올 것이고, 이 정보는 '대명사'에 대한 정보를 담을 수 있다.
예를 들어

다음과 같은 문장을 번역하고자 할 때, 저 'it'이 무엇을 가르키는지에 대한 정보를 담아주어야 한다.
이때 self attention을 하면 각 단어에 대해 나머지 단어들이 얼마나 유사한 지를 알 수 있다.

다음과 같이 query가 it일때, it이 The animal과 가장 유사하다는 것을 표현할 수 있다.
하지만 문제가 있다.
이전 RNN기반 셀에서는 은닉상태를 Key, Query로 사용하였다.
이제는 더이상 RNN을 사용하지 않는다.
그러므로 이 셀프 어텐션은 기존의 어텐션 기법과 살짝 다르다.
두개를 비교해보자.
|
기존의 어텐션
|
셀프 어텐션
|
|
|
Query
|
디코더 셀에서 은닉상태 하나
|
하나의 단어 임베딩 벡터와 가중치 행렬을 행렬곱한 벡터
|
|
Key
|
인코더 셀에서 은닉상태 하나
|
하나의 단어 임베딩 벡터와 가중치 행렬을 행렬곱한 벡터
|
|
Value
|
인코더 셀에서 은닉상태 하나
|
하나의 단어 임베딩 벡터와 가중치 행렬을 행렬곱한 벡터
|
완전히 다른점이 있다면, Value가 다르게 생성된다는 점이다.
|
기존의 어텐션
|
셀프 어텐션
|
|
인코더 셀에서 은닉상태 하나, 즉, 한 단어에 대한 Key벡터와 Value 벡터는 동일한 벡터를 사용한다.
|
Value 벡터은 Key 벡터는 서로 다른 가중치 행렬에
의해 생성되었다.
|
어텐션을 이야기로 풀어보면,
어느날 집에 a, b c 라는 세 명의 사람이 차례로 찾아왔다.
다음날, d라는 사람이 집에 가장 먼저 찾아왔는데, 다음 번에 올 사람이 누구일까? 라는 것을 예측하는 작업을 한다.
이때, 어제 a,b,c가 순서대로 찾아왔다는 정보는 예측 작업에 분명히 도움일 될 것이다.
그래서 d는 자기 이름과 a,b,c의 이름 사이의 유사한 정도 만큼, 각각 a,b,c가 가지고 있는 특성정보(직업, 나이, 성별 등등)을 참고하려고 한다.
그리고 이 비율에 맞게 참고하여 하나의 뭉뚱거린 정보를 가지고, 다음 번에 집에 올 사람을 예측하는 것이다.
이전에도 말한 적이 있는 Q,K,V 의 의미를 다시 한번 보자.
파이썬의 사전형태로써 Q,K,V는 다음과 같다.
Q : 현재 손에 들고 있는 (현재 처리 하고 있는) 정보
K : 각 정보들의 라벨 정보(정보를 담고 있는 파일의 이름)
V : 파일 안에 있는 정보
이미지로는 다음과 같을 것이다.

기존 어텐션에 빗대어 이해해보자.
Q : 현재 유사도를 구하고자 하는 특정 단어 은닉상태 벡터 하나
K : 모든 단어들을 라벨링 하였을 때의 각 단어들의 라벨을 뜻하는 은닉상태 벡터 하나
V : Key에서 이미 사용한 벡터를 Value 벡터로도 사용함(파일 이름과 파일 내용이 동일하다)
=> 하나의 Q와 모든 단어 K간의 유사도 정도에 따라
각 단어에 해당하는 Value(Key와 동일한 벡터를 사용한다)를 얼만큼의 비중으로 참조 할 것인지를 결정
=> 이 비중에 따라 Value(=Key벡터)를 가중합 하여서 하나의 벡터로 만든 것이 Attention 벡터
물론 모든 Q(output(decoder)에 입력된 모든 단어)에 대한 Attention 벡터들이 나옴으로 인해
이 Attention 벡터는 위에서부터 아래방향으로 Q의 갯수만큼 차곡차곡 쌓이게 된다.

셀프 어텐션에 빗대어 이해해보자.
Q : 현재 유사도를 구하고자 하는 특정 단어 하나
K : 모든 단어들을 라벨링 하였을 때의 각 단어 라벨 정보
V : 단어의 실제 정보
=> 하나의 단어 q에 대한 Key들에 대한 유사도 정도 만큼 각 단어에 해당하는 Value(≠Key)를 참조

최종 결과 벡터가 담고자 하는 의미는 같다.
'각 단어들이 얼마나 유사한가?' 라는 정보를 만들고 싶은 것이다.
본격적으로 Self-Attention을 해보자.

간단하게 2개의 입력에 대해 Self-Attention을 한다고 가정하자.
우리는 처음부터 Embedding 벡터를 가지고 Q,K,V 벡터을 미리 다 만든다.
(V를 미리 만드는 것에 대한 설명은 잠시 뒤 설명하겠다.)
X1과 Q 가중치 행렬 WQ, K 가중치 행렬 WK , V 가중치 행렬 WV을 각각 행렬 곱 하여서
q1, k1, v1 벡터를 만든다.
이때 차원이 축소가 되는데 사실 반드시 축소시켜야 하는 것은 아니다.
이것 또한 잠시 뒤 multi-head 개념을 설명 할 때, 추가적으로 설명하겠다.
q1, k1, v1 벡터의 역할을 앞에서도 말했지만, 다시 한번 집고 넘어가자.
q1 : 유사도를 구하고자 하는 특정 벡터 하나
k1 : X1 단어를 가리키는 이름 벡터
v1 : 단어 X1 의 진짜 정보를 담고 있는 벡터
일단 q1, k1, v1 벡터 모두 X1으로 부터 생성되었으므로, X1의 정보를 담고 있다.
우리는 X1의 정보를 3개의 역할로 분해하여 따로 저장한 다음 이를 이용하는 것이다.
이제 유사도점수(Score)를 구해보자.
우리는 이전과 같이 Q와 K를 내적하여 유사도를 구한다.

X1에 대하여 유사도 벡터를 만들기 위해
1. q1을 잡고
2. [q1과 k1 내적, q1과 k2 내적 ] 하여 내적 정보를 Score에 저장한다.
(실제 정보인 v와 내적하는 것이 아닌 이름인 k와 내적한다.
이것이 가능한 이유는 k1 벡터는 X1으로 부터 생성되었기에 X1의 정보를 담고 있기 때문이다. )
이번에는 Score로 만든 벡터를 바로 softmax에 집어넣는 것이 아닌 (루트 dk)로 먼저 나누고 집어넣는다.
(그 이유는 gradients가 안정적으로 되었기 때문이라 한다)

저 dk는 Key 벡터의 차원(64차원)이다.
이제 Value 차례이다.
하지만 기본적인 Attention과는 달리 Value가 미리 생성되어 있다.
우리는 이 Value를 마치 기본 어텐션에서의 인코더 은닉상태처럼 사용 한다.
기본 어텐션에서는
인코더의 은닉상태와 디코더의 은닉상태간의 유사한 정도에 따라
디코더 부분에서 각 인코더 은닉상태를 얼마나 참조할 것인지를 (Q,k의 내적의 softmax값)을 곱합으로써 Scale조정을 하였다.
저 인코더 은닉상태가 단어의 실제 정보를 담고 있듯이, 이번에는 Value 값이 Self-Attention에서 같은 역할을 한다.
Q와K가 유사한 만큼 각 단어의 Value값을 참조하여 가중합을 할 것이다.
그로인해, 유사한 단어일 수록 그 단어에 해당하는 Value값이 Self-Attention vector에 짙게 함유되어 있을 것이다.

X1에 대해 가중합 하여 얻은 Attention vector가 z1이다.
+가중합이 가능한 이유

곱함으로 인해 비례, 반비례 정보를 담을 수 있다는 점이다.
하지만 저 작업을 각 단어마다 따로따로 하면 비효율적이다.
행렬을 사용하는 이유를 까먹지 말자.

어짜피 한개의 Encoder 안에서 Self-Attention은 같은 가중치 행렬을 공유하여 사용하므로,
X를 열방향으로 쌓으면(axis=0) 다음과 같이 결과도 열방향으로 쌓인다.

이후 V도 열방향으로 쌓아 곱해주면,
결과는 Attention벡터들이 열방향으로 쌓인 행렬이 나온다.
조금 더 세부적으로 시각화를 하면 다음과 같다.

이제 이 정보를 Feed Forward Neural Network(FFNN)에 넘겨주게 된다. (FFNN에 대한 설명은 글 아래 부분의 논문분석에 설명해 놓았다.)

하지만 이렇게 보면 저 z1, z2, z3가 한꺼번에 들어가서 서로 연관성을 가지게 될 것 처럼 보인다.
사실은 그렇지 않고 서로다른 FFNN으로 들어가서,
Self-Attention에서는 출력들이 입력들의 상호작용으로 만들어 진 것과는 달리 서로 독립적인 출력이 나오게 된다. 그리고 이 출력이 다음 인코더의 입력이 된다.

저 인코더의 파란색 출력 r1, r2는 다음 인코더로만 가는 것이 아닌 디코더의 Encoder-Decoder Attention에 사용된다.

이는 seq2seq의 Attention 모델과 비슷하다.
이때는 이전 Attention 모델처럼
디코더의 각 단어 Embedding 벡터를 가지고 Q,K,V를 만든 다음,
디코더의 Q에 대한 , 인코더의 K들간의 유사도 Score를 구하는 것만 다를 뿐, 나머지는 똑같다.

(I am a student => je suis etudiant 번역 ) 출처 : https://wikidocs.net/31379
지금까지가 전체적인 흐름이다. 이제 세부적으로 들어가 본다.
논문 속 transformer 구조를 다시 한번 봐보자.
알아야 할 것이 3개가 있다.
1. Multi-Head Attention
2. Masked Multi-Head Attention
3. Add & Norm

저기에는 Self-Attention이 아닌 Multi-Head Attention이라고 쓰여져 있다.
1. Multi-Head Attention이란 무엇일까?
지금까지 Self-Attention을 한 것을 Single-Head Attention이라고 부른다.
이름처럼 Multi-Head Attention은 저 Self-Attention을 여러번 한 것이다.
모델 전체를 한번 생각해보자.
우리가 알고 있는것은 입력과 출력이고,
우리의 목적은 모델에 입력을 넣었을 때, 우리가 원하는 출력이 나오도록 교사학습 시키는 것이다.
이때 모델은 학습을 하게 되고,
학습한다는 것은 가중치들이 입력과 출력의 연관성에 따라 재배치 된다는 것이다.
Single-Head Attention에서는 하나의 인코더에 가중치 행렬을 3개 사용하였다.
[ Q 가중치 행렬 WQ, K 가중치 행렬 WK , V 가중치 행렬 WV ]
만약 같은 정보를 가지고 서로다른 2개의 Attention을 진행하면 어떨까?

다음과 같이 가중치 행렬 3개를 더 사용하여, 그에따른 Q,K,V를 얻고 Attention을 따로 진행한다면
2개의 Attention 행렬인 Z0, Z1이 나올 것이다.
논문에서는 8개의 Head를 사용했다.

이런 작업을 통해 얻는 이점은,
서로 다른 관점에서 문장 내 각각의 단어 유사도 정보를 뽑아 낼 수 있다는 점이다.
그리고 단순히 매개변수를 늘리는 효과도 지닌다.
이제 이 Z들을 합친다.

여기서 아까 q1, k1, v1 벡터를 만들 때,
차원이 축소가 이루어진 이유가 나온다.
논문 속에서 Embedding 벡터의 차원은 512이다.
그런데, Attention head Z의 차원은 가중치 행렬을 곱해서 얻은 Q,K,V와 같다.
게다가 나중에 Head들을 더한 Z의 차원은 (Head 개수) x (Z 하나의 차원) 이 될 것이다.
하지만, 같은 형태의 Encoders와 Decoders를 사용하므로 출력의 차원이 입력의 차원과 같아야 한다.
즉, 출력의 차원이 입력(Emebedding)의 차원인 512가 되어야 하는 것이다.
그렇다면 Z 하나의 차원은 Head의 개수만큼 나눠준 만큼을 가져가야 한다.
논문에서는 Head가 8개이므로 Z 하나의 차원이 64(8 x 64 = 512)가 된 것이고,
Z 하나의 차원은 Q,K,V와 같으므로 아까 dk(Key의 차원)가 64가 된 것이다.
+하지만 아까 반드시 차원을 축소 할 필요는 없다고 했는데, 그 이유를 생각해 보면,
그냥 어떤 차원이 나오든 간에 가중치 행렬을 거치게 하여서 차원을 내가 원하는 대로 맞춰 줄 수 있기 때문처럼 보인다.
마지막으로 다음과 같은 가중치 행렬을 곱해주면

사실 위 그림이 잘못된게 Wo는 정방행렬이다. (가로와 세로의 길이가 같은 정사각형 행렬)
가로도 입력 차원인 512여야하고, 세로도 모든 z들의 합차원인 512여야 하기 때문이다.

그로 인해 얻은 행렬 Z는
벡터 Z1, Z2, Z3 ..... 들이 위에서부터 하나씩 쌓인 것이다.
Zi : i번째 단어를 Q로 하였을 때, 계산한 각각의 단어들(Key)의 유사도를 담은 벡터
ex) i=1 일 때 => Z1 = [ ( 1 vs 1) ,( 2 vs 1), ( 3 vs 1) , ( 4 vs 1), ... , ( n vs 1) ]
( n : 입력 단어 개수), Z : n차원 벡터
그리고 이 Z 행렬은 모든 Head에서 얻은 attention 정보를 함축해서 담게 된다.
한 눈에 보기 쉽게 나타내면 다음과 같다.

각 Head 에 대한 [Z1, Z2, Z3 .....] 들이 어떤 값을 가지고 있는지 시각화 해보면,
(짙은것이 높은 값, 연한것이 낮은 값)
2개의 Head를 사용하면 다음과 같고

8개의 Head를 사용하면 다음과 같다.

더 다양한 Attention 정보들을 함유하고 있음을 볼 수 있다.
2. Masked Multi-Head Attention이란?
사람들은 얼굴을 가리기 위해서 마스크를 쓴다. 코드도 똑같다.
코드를 공부해본 사람이라면 기초부분에서 masking을 배운다.
mask는 0과 1로 이루어져 있으며
0인 경우 데이터를 없에고, 1인 경우 데이터를 흘려보내 체로 걸러내는 듯한 역할을 한다.
데이터에 0을 곱하면 0이 되고, 1을 곱하면 데이터 원본이 되는 성질을 이용한 것이다.
ex ) 원 데이터 : [ a , b , c , d ]
마스크 : [ 1 , 0 , 1 , 0 ]
=> 두 벡터의 원소 별 곱 => [ a , 0 , c , 0 ] : a와 c만 걸러졌다.

모델 구조 그림을 다시 보면 디코더의 처음 Multi-Head Attention에서만 Masked 가 된 것을 볼 수 있다.
번역기를 예로 들면,
우리는 원문을 번역 하기 위해 원문 입력 문장 전체를 받아 온다.
하지만, 디코더에서는 인코더에서처럼 전체 문장을 입력으로 한번에 받으면 안된다.
디코더에서는 입력받은 단어들에 대한 다음 단어 예측이 목적이기 때문에
전체 문장을 다 받아오면 미래 시점의 단어까지 참고해버린다.
이를 막기 위해 첫번째 attention층에서는 mask를 사용한다.
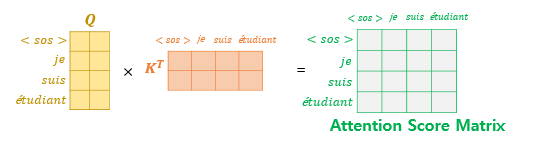
디코더의 <sos> (start of sentence)가 포함된 입력에 따른 Self-Attention을 진행하면
초록색 Attention Score Matrix를 구할 수 있고

미래 단어에 대한 단어들은 masking 행렬(살리는 정보 :1, 죽이는 정보 : 0) 곱을 이용해 masking을 해준다.
이것도 기존 셀프 어텐션과 똑같이

다음과 같은 과정을 거치고 Z를 여러개 만들고 합치고 가중치를 곱하는(Multi-Head)과정을 거치고
최종 Z를 얻게 된다.
그 Z행렬은 Z1,Z2,Z3,... 들이 위에서부터 하나씩 쌓인 행렬일 것이다.
그 Z1,Z2,Z3,... 들이 초록색 선을 따라 입력으로 들어간다.
이후 그 입력에 따른 Q,K,V 행렬을 만든다. (디코더의 Q,K,V)
그중에서 디코더의 Q를 사용하고,
인코더의 출력에서 나온 Z를 가지고 만든 K와V를 사용하여 Multi-head Attention을 진행한다. 이는 기본적인 seq2seq Attention과 유사하다.

그때의 Single-Head Attention은 다음과 같을 것이다.

마지막으로
3. Add & Norm 이란?
말 그대로 add하고, Normalize하는 과정이다.

Add(잔차 연결: Residual connection)는
입력벡터들을 작업 이후에 한번 더 더해주는 것이다.
X와 Z는 차원이 같은 벡터들을 쌓은 행렬이므로 더하는 것이 가능하다.
위 그림에서 X + Z가 Add를 뜻하고,
이를 통해 하위 층에서 학습된 정보가 데이터 처리 과정에서 손실되는 것을 방지할 수 있다.
Add 이후에는 Layer Normalization(층 정규화)을 진행한다.
X와Z를 더한 행렬이 다음과 같다면

행 방향으로 평균과 분산을 구한다.
이후 행 벡터마다 해당하는 평균을 그 행 벡터의 각 원소마다 빼주고, 표준편차로 나눠주면,
각 행마다 평균 = 0 , 분산 =1 을 만들어 줄 수가 있고 정규화가 된다.
정규화된 각 행 벡터들을 (xi hat) 이라고 하자.
이후 추가적으로 학습 가능한 매개변수인 감마와 베타를 준비한 이후

각 행에 해당하는 벡터 (xi hat)에 대해 다음과 같이 추가 작업을 해주면

출력이 Add & Norm 을 거쳐 다듬어진다.
이 Add & Norm 을 멀티 헤드 어텐션을 거친후, FFNN을 거친 후 각각 해준다.

추가적으로 다음 그림에서는 인코더와 디코더가 하나이다.
만약 여러개의 인코더와 디코더가 쌓인다면 입력과 출력의 흐름은 어떻게 되는지 알아보자.

인코더는 입력에 대해 모든 인코더 층을 거친 결과를 가지고
모든 디코더에서 Encoder-Decoder Attention에서 사용 됨을 알 수 있다.
최종적으로 흐름을 정리한 gif이다.


2. 자세한 논문 리뷰

=> RNN CNN 인코더 디코더 사용하지 않고 Attention만 이용하였고, BLEU(기계 번역 품질 평가)에서 좋은 결과를 얻음.


=> 기존 RNN단점이 극복이 안됨 => Attention만을 이용해 병렬화 가능하게 하고, 문장 길이에 강인하게함



인코더, 디코더 , attention은 위에서 구현한 구조와 일치한다.
Decoder에 masking이 눈에 띈다.
making을 한 이유로
'This masking ensures that the predictions for position 'i' can depend only on the known outputs at positions less than 'i'.
와 같이 이전에 말한 대로 decoder에서는 i번째 단어에 대한 다음 단어를 예측할 때, i 이전의 단어들에 대한 정보만을 이용해 다음을 예측하려 했음을 알 수 있다.

Scaled dot인 이유는 dot(내적)한 값을 루트 dk로 나눠 scale 조정을 했기 때문이다.

식으로 보면 다음 Attention과 같고, 이미 앞에서 본 식이다.
그리고 루트 dk로 나눠준 이유가 더 정확히 나온다.
먼저 가장 많이 사용되는 Additive attention과 dot-product attention 중에 dot-product attention을 쓴 이유는, 더 빠르고 연산에 필요한 메모리를 덜 쓰기 때문이다.
먼저 additive attention이란 무엇일까?

스코어 함수가 다음과 같은 attention이다.
h는 인코더 은닉층, s는 디코더 은닉층, Wa와va는 변수(parameter)이다.
그런데 루트 dk로 스케일 조정을 안해주면 additive attention이 더 성능이 좋았지만,
dk가 너무 커버리면(Key의 가중치 행렬의 열공간 차원 = dk)
dot-product 값들이 너무 커져서 gradient가 극단적으로 작아진다는 것이다.
이에 대한 이해를 하려면 softmax함수의 학습 문제를 알아야 한다.

인풋이 불필요하게 크다면 이는 잉여값이 포함되어 있다는 말이다.
(각 변수들 간의 차이점만 나타낼 정도의 크기면 되는데, 모두 너무 커버리면 서로 그게 그것이 되버린다.)
이 과정에서 W가 학습이 되지 않는 이유로써 gradient가 극단적으로 작아지기(=>학습 속도가 극단적으로 느려진다) 때문임을 알 수 있다.


multi head attention에 대한 부분이다. head들을 concatenate하는 것을 볼 수 있다.
이를 통해 병렬화가 가능해져 더 많은 정보를 함축하는 것이 가능해졌다.

세 부분에서 multi-head attention 사용.

Positiob-wise Feed-Forward Networks에 대한 내용으로써,
아까 FFNN의 대한 내용이다. 활성함수로는 ReLU를 사용했다.

Z1하고 Z2는 서로 각자 FFN을 거쳤지만, W1,W2,b1,b2는 서로 공유하고 있음을 알 수 있다.
그리고 저 max를 취하겠다는 뜻이 ReLU를 취하겠다는 말과 동일하다.
그리고 저기에
'Another way of describing this is as two convolutions with kernel size 1. '
부분이 무엇인지 생각해보면 다음과 같다.

kernerl size(filter size)를 1로 하여서 convolution을 하면 각 z1,z2에 대해 channel을 하나 얻을 수 있다.
이를 2048번 하면 맨 아래의 행렬처럼 될 것이고 이 벡터가 위에서 얻은 2048차원의 벡터를 쌓은 것과 같다.

반환 부분도 똑같은 방법으로 이해 가능하다.


recurrence와 convolution을 쓰지 않았기 때문에, 임베딩 부분에 positional encoding을 해주었다.
위의 표는 Layer type에 따른 complexity이다.
이는 sinusoidal(사인파) 버전을 택하였고, 두 PE는 선형 연산을 통해 구해질 수 있다는 점은 서로서로 상대적인 위치를 모델이 학습하는데 이점을 줄 것으로 가정했다고 한다.


Self attention을 택한 이유를 설명한다.
1. 각 층의 computational complexity
2. 병렬 처리 가능한 computation의 양
3. 단어 간 먼 거리에도 관계를 구하는데 있어 강인함


standard WMT 2014 English-German dataset 이용,
r WMT 2014 English-French dataset 이용,
8개의 NVIDIA P100 GPU 사용,
optimizer는 adam 사용


1.sub-layer 출력에 대해 dropout 진행, add & norm 전에 dropout 진행
2. positional encoding 과정에서도 dropout,
3. Label Smoothing 0.1 사용, 잘못된 라벨링이 있을 수 있으므로, 90퍼센트의 확신을 가지고 라벨을 사용하겠다는말이다. => 10퍼센트는 다른 라벨로 인식하게 됨 => BLEU 증가.(model generalization 해주어서)
Table 2 : 결과
Transformer big version이 sota를 찍고 있다.
+ BLEU 점수에 관하여..



저 노란색들이 Hyperparameter들이고, 그에 따른 점수이다.

결론. recurrent,convolution보다 빠르다.
'Tensorflow 2 NLP(자연어처리) > 사전학습 모델' 카테고리의 다른 글
| GPT-1(Improving languague understanding by Generative Pre-Training)란?+벡터 흐름 하나하나 자세하게 설명 및 논문 리뷰 (2) | 2022.10.10 |
|---|---|
| [5-4] Attention Mechanism(어텐션 메커니즘)이란? (0) | 2021.11.14 |
| [5-3] 시퀀스-투-시퀀스(Sequence-to-Sequence)란? (0) | 2021.11.13 |
| [5-2] ELMo란? (0) | 2021.11.13 |
| [5-1] Six challenges(benchmarks) in NLP (0) | 2021.11.13 |