비용함수로 자주 사용되는 Cross Entropy에 대해서
깊은 이해를 하게 해주는 영상을 발견했다.
( 자막도 잘 나와있어서 좋다. )
| 정보량
세상에는 다양한 종류의 정보들이 있다.
이 정보들을 하나의 기준으로 평가하고 싶은데
어떤 기준이 좋을 것인가?
A라는 사람이 B라는 사람에게 정보를 전달할 것인데
보내고자 하는 정보의 양(정보량)을 수치화 할 수 있는 방법이 있을까?
일단 정보들을 하나의 기준으로 평가하려면
정보들을 전달하는 방식이 동일해야 할 것이다.
어떤 정보는 문자로 보내고, 어떤 정보는 숫자로 보내면
이 둘 정보의 차원이 다르기 때문에
정확한 양의 차이를 가려내기가 힘들기 때문이다.
그래서 선택한 방법이
어떤 정보를 보낼 것인데
" 현재 전달하고자 하는 정보를 완벽히 표현 가능한 최소한의 Yes or No 질문 횟수 "
를 판단 기준으로 삼고
각 정보를 완벽히 표현하기에 충분한 최소 질문 횟수를 정보량이라고 칭하자는 것이다.
정보의 복잡도가 높고 양이 많을 수록
정보량이 많기에
질문의 횟수가 늘어난다는 아이디어에서 착안한 것이다.
예를들어
10개의 동전 앞면,뒷면 등장 횟수 정보를 전달하고자 한다면
1(Yes)을 앞면이라하고, 0(No)을 뒷면이라 정한다음에
만약,
[ 앞,뒤,뒤,앞,앞,앞,뒤,앞,뒤,뒤 ] 라는 정보를 전달하고자 한다면
[ 1, 0, 0, 1, 1, 1, 0, 1, 0, 0 ] 라는 10번의 질문만 하면 된다.
하지만 6개의 알파벳을 보내려고 한다면 좀 더 복잡해진다.
이때, Yes or No 질문으로 26개의 알파벳 중에 하나를 특정하려면
내가 찾고자 하는 알파벳이 내가 나눈 집합 안에 들어있는지 아닌지를 Yes or No를 통해 반복하면서
구해나갈 수 있다.
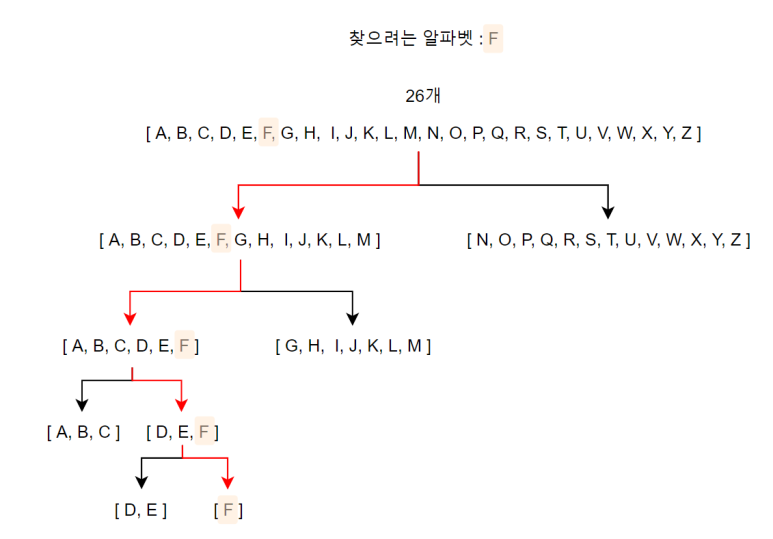
위에 처럼 매번 반씩 쪼개어서
찾으려는 알파벳이 앞쪽 집합에 있는지, 뒷쪽 집합에 있는지에 따른
Yes or No 이진 선택(binary selection)을 통한 범위 좁혀나가기를 하다보면
4, 5번이면 내가 원하는 집합을 찾을 수 있음을 볼 수 있다.
우리는 하나의 알파벳을 표현하기 위해
왼쪽 선택을 1, 오른쪽 선택을 0이라 한다면
[ 1, 1, 0, 0 ] 이라는 정보를 보내주면 된다.
이때, 어떤 정보든지
이진(binary) 선택 방식을 통해 표현하고자 할 때,
최소 선택해야 하는 횟수를 한번에 구할 수 있는 식이 있을 까?
다음을 한번 생각해보자.

2의 지수가 의미하는 바를 깊게 생각해 보면
내가 이진 선택 방식으로 하나의 값을 얻어내기 위해서
필요한 최소한의 선택 횟수라는 것을 알 수 있다.
그렇기 때문에 우리는 아래와 같은 식을 쓸 수 있다.

위의 예시를 대입해본다면
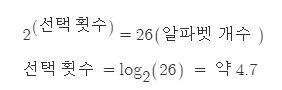
약 4.7번 선택해야 한다는 값이 나온다.
아까 보았듯이 4번 만에 구할 수 도 있고, 5번이 필요한 경우도 있었다는 사실로 확인 가능하다.
이제 우리는 6개의 알파벳을 보내려고 한다면
하나를 보내는데 4.7번 선택해야 하므로
6 x 4.7 = 28.2 번 선택해야 한다는 것을 알 수 있다.
동전 앞뒤 정보를 보내는 것보다 훨씬 많은 정보량을 요구한다는 것을
이제야 정확히 판단 할 수 있게 되었다.
이제 이 식을 좀더 범용화 한 것이 아래의 식이다.
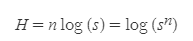
log 내의 s는 선택 가능한 샘플이라고 할 수 있고
n은 전달하려는 정보의 개수이다.
이때의 H를 정보량이라고 정의한다.
| 엔트로피
앞선 Yes or No 선택과정에서는
각 샘플들을 모두 동일한 가치( 내가 원하는 알파벳일 가능성 )를 지니는 것으로 간주했기 때문에
확률이라는 개념이 선택에 포함되지 않았다.
하지만 아래와 같은 경우는 어떠할까?
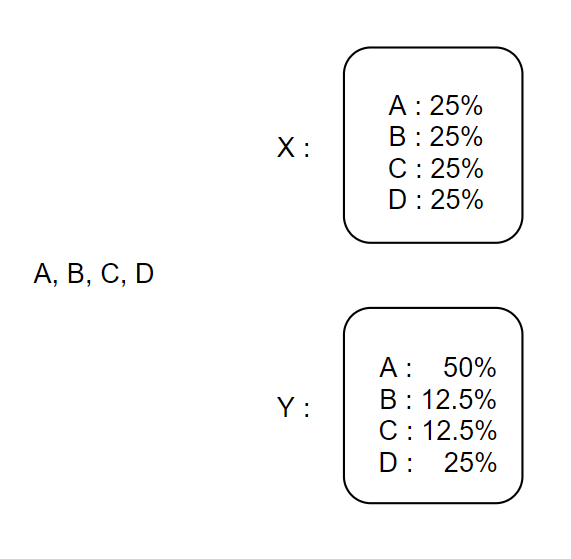
A, B, C, D를 출력하는 X, Y라는 모델이 있는데
X모델의 경우 각각을 같은 확률로 출력하고
Y모델의 경우 위에 표시된 확률에 따라 출력한다.
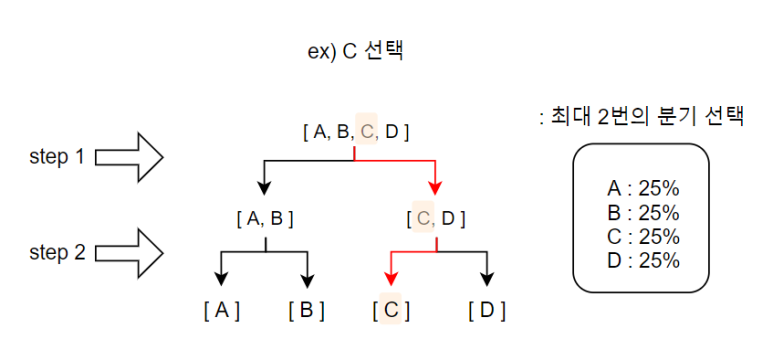
X모델 같은 경우 찾고자 하는 알파벳이 어떤 것이든지
최대 2번만 선택하면 찾을 수 있다.
이때, 주의깊게 볼 것은
분기를 나누는 최적의 가지를 때, 양쪽의 선택 확률합이 서로 같아야 한다는 것이다.
( EX) 맨 처음 분기 A+B = 50%, C+B= 50% )
만약 다를 경우에 아래와 같은 문제가 발생한다.
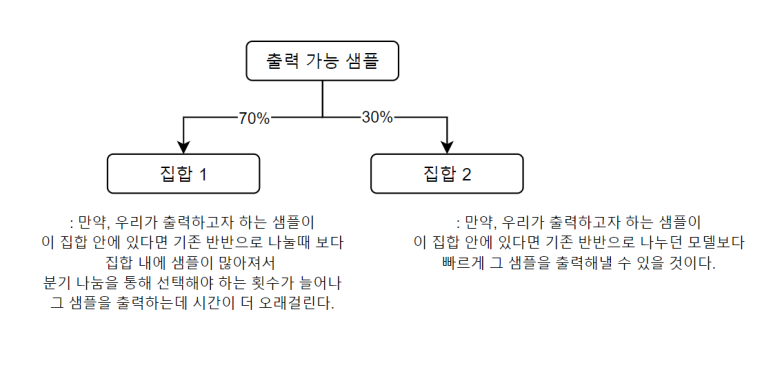
한쪽으로 치우칠 경우에는 쓸모없는 선택이 늘어날 수가 있다.
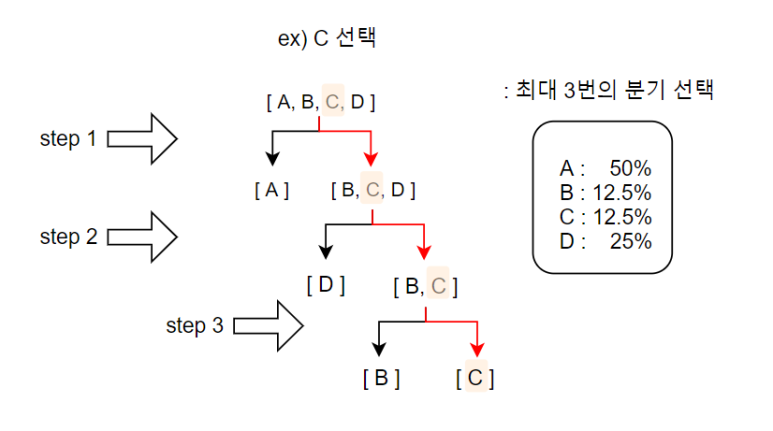
Y모델 같은 경우 찾고자 하는 알파벳이 어떤 것이든지
최대 3번만 찾으면 된다. 즉, 3번의 선택만 하면 모든 알파벳 출력을 분류 가능하다는 것이다.
이전보다 선택 횟수가 많아졌으므로 정보량이 더 많은 모델인가?
아니다. 아직은 판단하기 이르다.
A와 같은 경우는 1번의 선택으로도 발견 가능하기 때문에
그래서 우리는 평균적인 선택 횟수를 얻어낸 다음에
그 선택 횟수를 모델을 대표하는 정보량으로 간주해야 한다.
최대 횟수가 올라간 이유를 찾아보자면
이때, 분기를 나누는 가지를 내는 과정에서
확률 합이 동일한 두 집단으로 나누도록 하는 분기 나누기가 진행되었기 때문이다.
이렇게 선택 과정에서 확률이 포함되어 버리면
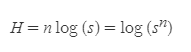
앞에서 구한 위 식을 통해 선택 횟수를 얻어낼 수 없다.
우리는 평균 선택 횟수를 원하는 것이다.
새로운 아이디어가 필요하다.
이렇게 하면 어떨까?
완전히 다른 관점에서 모델을 바라보는 것이다.
정보량을 모델의 평균 깊이(Depth)로 생각해보자.
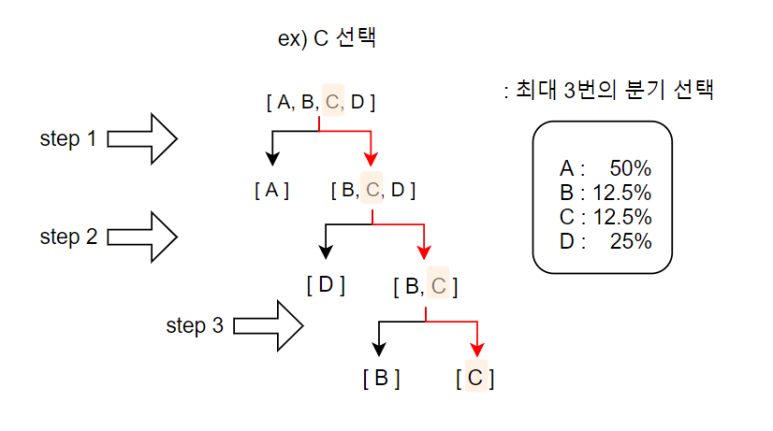
Y 모델같은 경우, 위의 확률대로 A,B,C,D를 출력하기에
이에 따른 Tree를 만들 것인데 이 Tree는 최소 선택을 하기 위한 최적의 분기 형성이 이루어져 있다.
( 원소의 확률 합이 동일한 두 집합으로 나뉘도록 분기를 구성한다 . ex) {A} : 50% , {B,C,D} : 12.5+12.5+25 = 50% )
이 Tree를 따라 출력된 1000개의 샘플을 확인해보면
이론상
A는 500개,
B,C는 각각 125개,
D는 250개가 나왔을 것이다.
출력 과정을 시각화 해보자면
맨 위에서부터 가지를 타면서 내려오면서 leaf node(마지막 지점)에 도달한 것을 출력할 것인데,
A는 선택을 1번만 하면 출력 되고,
B,C는 선택을 3번 해야 출력되고,
D의 경우 선택을 2번 해야 출력된다.
이 선택(step) 횟수를 Tree의 깊이라고 생각한다면
이 모델의 출력값들이
평균적으로 Tree 내부에서 분기 선택하는 횟수를 우리는 아래와 같은 식으로 나타낼 수 있다.
1000개 샘플 기준
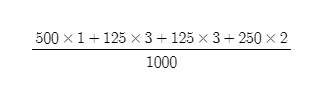
= P(A)x( 1 ) + P(B)x( 3 ) + P(C)x( 3 ) + P(D)x( 2 ) = 1.75
이 값이 의미하는 바가 무엇일까?
Y 모델에서 나온 출력들의 Tree 내에서 진행되는 선택 횟수에 대한 기댓값이다!
이때 선택 횟수를 Tree를 깊이 들어가는 정도라고 생각 할 수 있다.
즉, 광부가 땅을 파서 광물을 얻으려 하는데
"어떤 광물이든지 상관없이" 광물을 얻기 위해서 평균적으로 파내야 하는 깊이라고 이해하면 된다.
그리고 우리는 깊이 들어가기 위해 불확실성을 안고 선택을 해야하기 때문에
이 값을 우리는 엔트로피(Entropy)라고 한다.
굳이 깊이 들어가지 않아도
광물이 잘 나오는 모델, 그런 확률분포를 가지는 샘플들을
우리는 엔트로피가 낮다고 말하고
정보량이 낮다고 말한다.
+ 추가적으로 선택횟수는 또 각 샘플의 등장 확률과도 연관이 있음을 볼 수 있다.
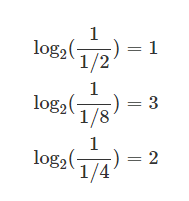
각 확률의 역수를 log에 집어넣으면
그 출력의 Tree 내에서의 필요 선택 횟수가 나오는 것을 확인할 수 있다.
그래서 우리는 아래와 같은 식을 얻을 수 있다.

H라는 엔트로피를 통해
X와 Y 모델을 수치화 한 결과
X = 2, Y = 1.75 가 나왔다는 것은
Y의 엔트로피가 작다는 뜻이고,
더 적은 정보량(= 총 선택의 횟수 = 해당 정보를 온전히 표현하는 데 필요한 최소 선택의 횟수)을
생산하는 모델이라고 볼 수 있다.
이제 엔트로피를 정리해보자
어떤 모델의 엔트로피라 함은
모델에서 어떤 값을 출력하고자 할 때,
그 출력물이 모델 내부에서 거친 평균적인 최적의 이진 선택 횟수라고 말할 수 있고
엔트로피가 준다는 의미는
평균 선택 횟수가 줄어든다는 뜻이므로
생성하는 정보량이 줄어든다고 볼 수 있다.
이제 이 엔트로피를
Cross Entropy로 확장해본다.
앞선 모델 Y를 다시 가져와보겠다.
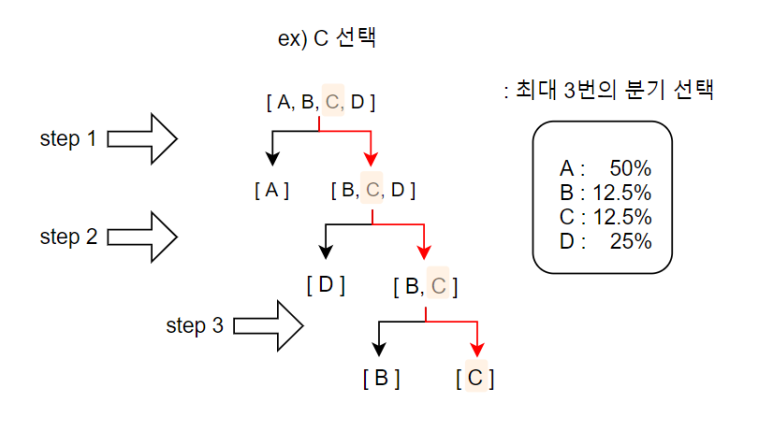
각 분기를 통해 반반씩 분할하여 선택하기 때문에
최적의 선택 Tree가 만들어 진 것을 볼 수 있다.
만약 여기에
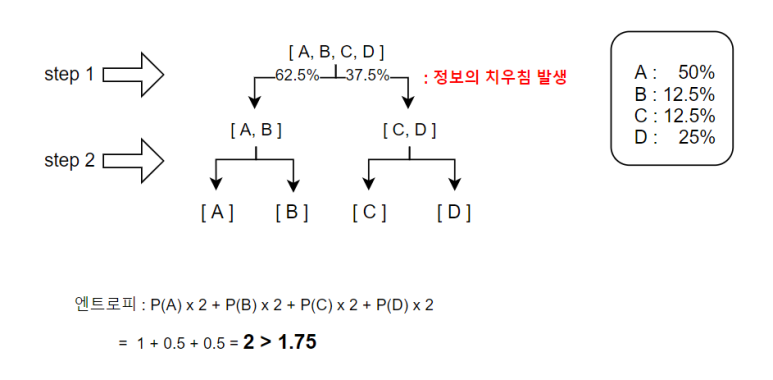
위와 같은 방식으로 분할한다면 어떨까?
정보의 치우침으로 인해
( 주의! 각 방향으로 나뉨에 따라 분리되는 정보의 양이 달라졌다는 것이지, 각 방향의 선택 확률이 달라졌다는 것은 아니다. 이진 분류이므로
각 방향으로 갈 확률은 둘 다 동일하게 50%이다. )
쓸모없는 선택이 생겼고
( A라면 한번의 선택만으로도 분류 가능한데 이번 같은 경우 2번의 선택을 진행했다. )
엔트로피가 증가했다.
( 출력의 모델 내 평균 선택 횟수가 증가했다. )
즉, 최적의 Tree를 만들어야지만
그 모델의 최소의 엔트로피를 얻어낼 수 있다.
| Cross Entropy

아까 우리가 정리한 엔트로피 식이다.
pi 는 샘플의 출력 확률이고
-log2(pi)는 각 샘플의 모델 내 최소 분기 선택 개수이다.
근데 -log2(pi)를 구성하는 pi와
앞에 있는 pi는 성격이 조금 다르다
앞에 있는 pi는 각 샘플의 출력 확률 그 자체를 나타내지만
log2( ) 내에 들어가는 pi는
Tree 내에서 가지치기에 방식에 따라 부여되는 확률값이다.
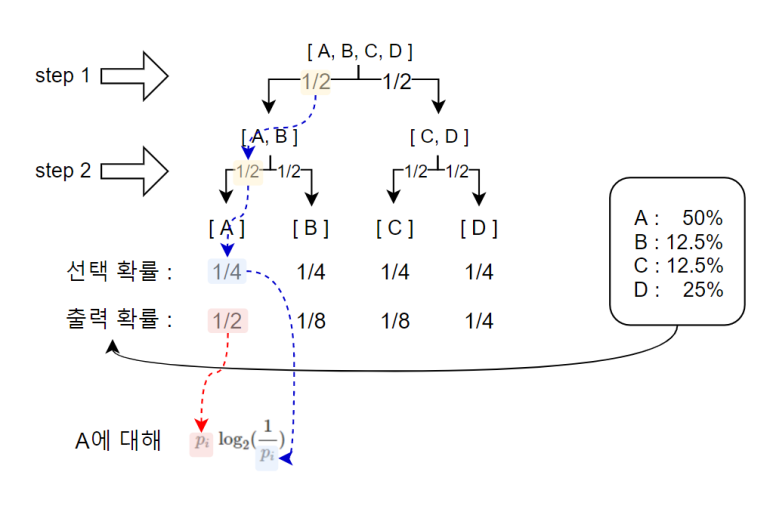
그림으로 보면 위와 같다.
만약 최적 Tree가 아닌 경우에는
저 pi 두 개를 서로 다른 값으로 바꿔줄 필요가 있다.
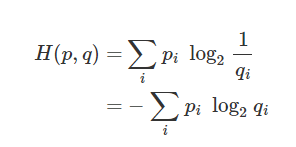
출력 확률을 pi 로 하고,
Tree 구조에 따라 조건적으로 생기는 선택 확률을 qi 라고 하고 위와 같이 정의해보았다.
그럼 이제 어떻게 해야만 엔트로피(H)를 줄일 수 있을까?
pi는 샘플 데이터의 분포 정보이기 때문에 변하지 않기에
엔트로피를 줄이기 위해 변화시킬 수 있는 것은
Tree 구조를 바꿔서 qi를 바꾸는 것이다.
그리고 우리는 앞서
최적의 Tree의 경우
pi와 qi의 구분을 없이 사용하였다는 것을 알고 있다.
그러므로 최적의 Tree를 만들기 위해서는
qi가 pi가 되도록 만들면 된다!
즉, qi가 학습할 수 있는 모델이라면, pi가 되도록 학습시킨다면
엔트로피(H)를 줄이고 우리가 원하는 목적에 최적화된(Optimized) 모델을 얻을 수 있다.
이러한 특성을 활용해
인공지능 모델 학습 시에 Cross entropy를 사용한다.
+ 확률분포가 이산형이 아니라 연속형이라면 아래와 같이 integral 형태로 변환하면 된다.
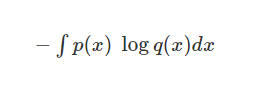
이제 진짜 Logistic Regression에서 사용하는 Cost Function을 살펴보자.
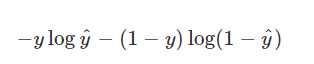
y : 실제 라벨 ( 0 or 1 )
ŷ : 예측 라벨
Cross entropy function이라고 우리가 학습 시에
가중치를 업데이트 하기 위해 편미분 할 때 사용하는 식이다.
이 식을 살펴보면
직관적인 해설
- 실제 라벨이 1인 경우
앞의 항만 살아남아서
- log(ŷ) 가 Cost가 되는데
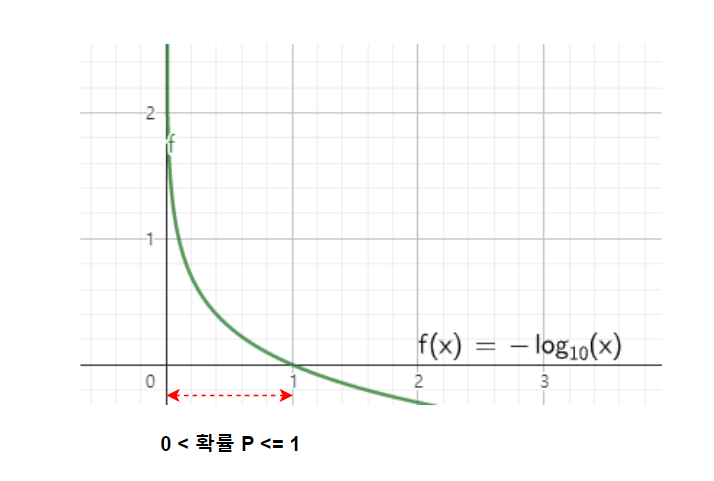
예측값이 1에 가까워질수록 Cost가 줄어드는 형태이다.
- 실제 라벨이 0인 경우
뒤의 항만 살아남아서
- log(1-ŷ) 가 Cost가 되는데
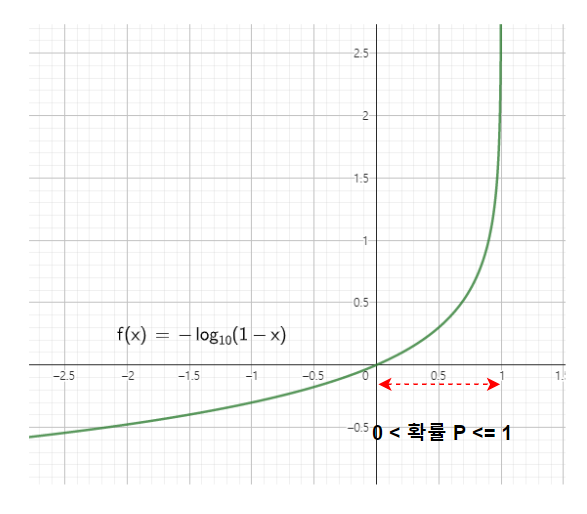
예측값이 0에 가까워질수록 Cost가 줄어드는 형태이다.
Cross entropy 관점
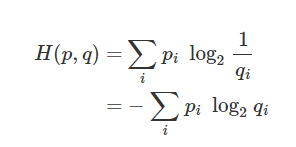
qi가 pi에 따라가도록 학습시키는 것인데
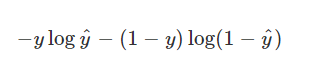
위의 식에서
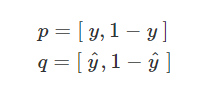
p와 q를 다음과 같이 생각할 수 있어서
y : 실제 라벨
ŷ : 예측 라벨
에 대해
ŷ가 y로 되도록 학습(optimize)시키고
1-ŷ 가 1-y가 되도록 학습(optimize)시킨다.
모든 것이 맞아 떨어진다...!
끝.
'Tensorflow 2 NLP(자연어처리) > 추가적으로 필요한 개념' 카테고리의 다른 글
| Automatic Differentiation이란 (0) | 2022.10.23 |
|---|---|
| PCA(주성분분석)의 목적함수 증명 (0) | 2021.11.15 |
| [1-6] 도커(Docker)에서 파이썬(python)코드로 작업하기 (0) | 2021.11.12 |
| [1-5] 최대우도법 (0) | 2021.11.12 |
| [1-4] DAN(Deep Averaging Network)란? (+Dropout) (0) | 2021.11.12 |