인간은 지금껏 무언가를 생성해냄으로써 발전해왔다.
시간이 흘러
아날로그에서 디지털로 넘어감에 따라
컴퓨터라는 뛰어난 계산기는 드디어 인간을 모방하기 시작한다.
두려움을 느낀 인간은 대비책을 제시해 보았다.
" 인공지능(Artificial Intelligence)이 하지 못하는 분야인 독창성(creativity)를 키워야 한다! "
하지만 문제가 있다.
독창성이란 무엇일까?
사람이 진정으로 무(無)에서 유(有)를 만들어 낼 능력이 있을까?
인간이 만들어내는 모든 부산물들은
그 인간이 학습한 지식들에서 나온다.
학습한 지식을 그대로 따라하는 사람이 아닌
학습한 지식들을 합성하여
새롭고 더 탁월한 지식을 만드는 사람을
우리는 독창적인 사람이라고 부르는 것이 아닐까?
하지만 이 독창성의 영역을 인공지능이 침범한다.
GAN이다.
목차
GAN 요약
핵심 이해하기
자세한 목적함수 설명
한계점
GAN의 파생들
자세한 논문 리뷰(추가 예정)
코드 실습
GAN 요약
GAN은 학습한 이미지들을 바탕으로
새로운 이미지를 생성해낸다.
GAN의 이미지 생성의 유명한 예시가 있다.
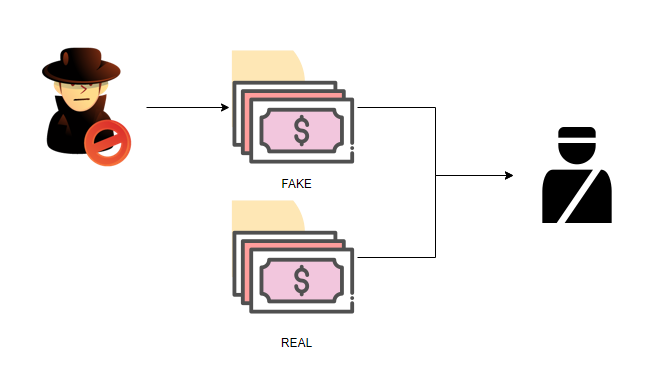
위조지폐범이 더 진짜같은 위조지폐를 만드려고 노력하는 동시에
경찰은 더 잘 구분하기 위해 노력한다.
위 과정이 반복됨에 따라
위조지폐범이 -> 위조지폐를 만들어내는 능력은 향상되게 될텐데
이 능력을 따로 분리해서
진짜와 비슷한 여러가지 지폐들을 생성하는데 사용하는 것이다.
핵심 이해하기
이미지 벡터화
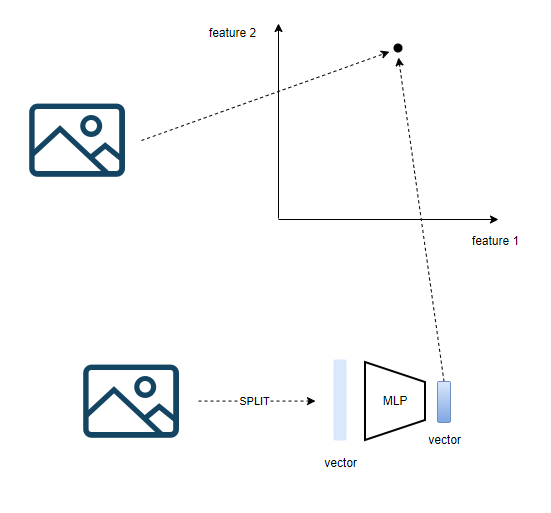
이미지의 경우 다차원 공간에 하나의 점으로 위치시키는 것이 가능하다.
여러개의 점은 직선이 되고,
여러개의 직선은 평면이 되는 원리에 의해
이미지의 한 픽셀에는 색깔정보가 담겨있다고 생각할수 있으므로
이미지는 여러줄의 '픽셀 벡터' 로 생각할 수 있다.
이 픽셀 벡터들을 한 줄로 길게 이어서
다층 신경망(MLP)을 통과시키면 하나의 벡터를 얻을 수 있다.
이 벡터를 공간상에 위치하면 끝이다.
이미지 벡터가 의미하는 것
앞서 만든 벡터가 의미하는 바가 무엇일까?
사실 랜덤 초기화된 다층 신경망에
이미지를 태워 보내는 것만으로 얻은 벡터는
딱히 어떠한 의미를 가지고 있다고 말하기 힘들다.
특정한 알고리즘을 통해 비슷한 특징을 가지는 벡터들은 비슷한 공간에 위치시키고
서로 다른 특징을 가지는 벡터들은 먼 공간에 위치시킨다면
그제서야 그 벡터는 의미를 가지고 있다고 말할 수 있을 것이다.
하지만 여기에서는 다층 신경망을 통과했을 뿐이다.
추가적으로 아래와 같은 작업을 해준다면
우리는 출력 벡터에 의미를 부여할 수 있다.
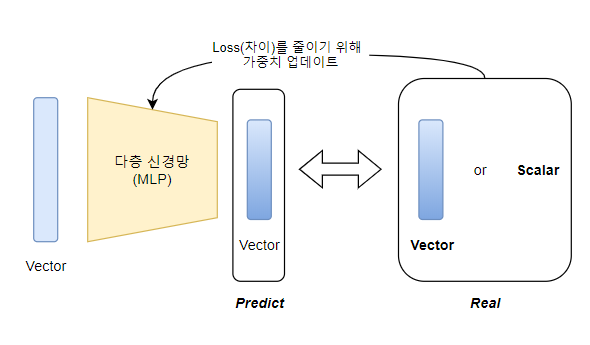
그러기 위해서 다층 신경망을 통과한 벡터와 비교할 수 있는
벡터 또는 스칼라값이 필요하다.
이는 입력 Vector을 넣었을 때, 내뱉은 벡터(예측값)에 대한 실제값이라 말할 수 있고
이 둘 간의 차이를 줄이게 하는 다층 신경망의 가중치를 찾아 업데이트 함으로써
다층 신경망은 입력 Vector안에 녹아있는 각 원소들간의
값과 패턴 정보에 적절히 반응하여
Real에 최대하게 유사한 값을 내뱉을 수 있게 된다..
이런 가중치 조정이 이루어진 이후에는,
입력벡터들 중에
서로 비슷한 특성을 가지는 벡터들은 => 다층 신경망을 거치고 비슷한 값을 내뱉게 될 것이고
=> 만약 내뱉는 값이 벡터라면 => 비슷한 공간에 위치하고 있게 된다.
이런 학습을 통해
우리는 비슷한 이미지는 비슷한 공간에 위치시키는 것이 가능한
다층 신경망(MLP)를 얻게 된다.
여러 이미지에 대한 확률 분포 생성
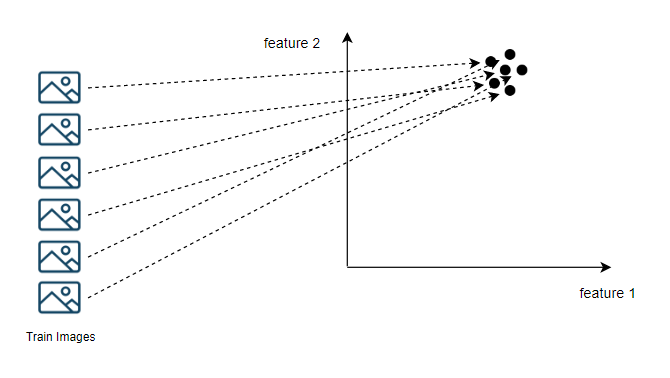
앞서 말한 방식대로 학습된 신경망에
이미지를 넣게 되면
비슷한 이미지는 비슷한 공간에 위치하게 된다.
이때 비슷한 이미지란, 비슷한 특징을 공유하는 이미지라고 생각할 수 있고
더 나아가 우리는 저 벡터들이 위치하고 있는 공간의
축 벡터들( 위 그림에서는 feature 1, feature 2 )을
이미지에 숨겨진 특성 정보를 수치화 할 수 있는 축이라고 여길 수 있다.
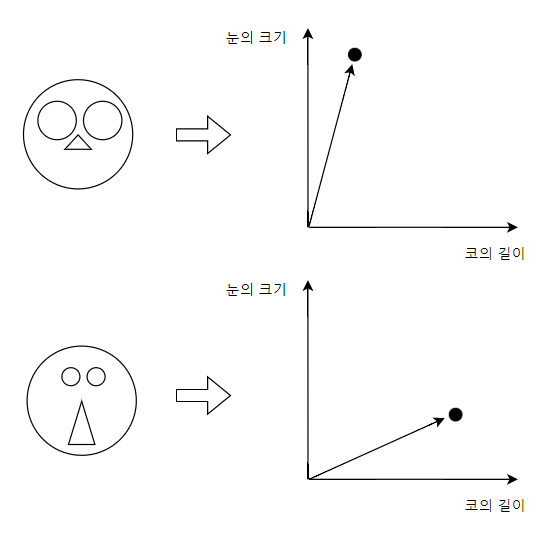
그래서 이미지 내에 비슷한 특징을 가지는 이미지는
벡터 공간상에 비슷한 위치에 존재하게 된다.
여기서 축의 개수( = 출력 차원 )가 많아질수록
고려할 수 있는 특징의 개수도 많아짐으로써
더 명확하게 이미지를 담을 수 있는 벡터가 된다.
이제, 많은 input을 넣음으로써
들어온 input들의 벡터들의 위치를 가지고
확률분포를 생성할 수가 있다.
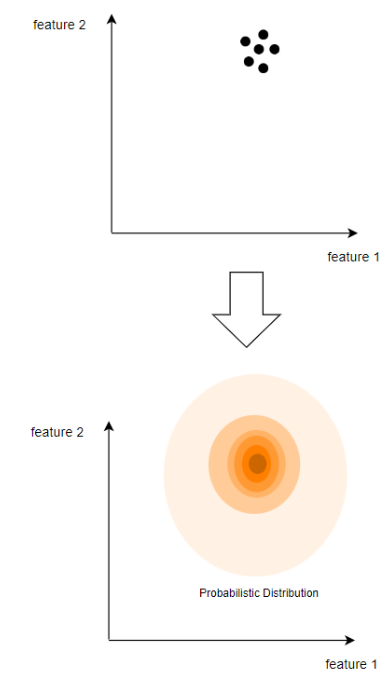
자주 등장하는 위치일수록
입력 이미지들의 대표로 간주할 수 있는 좌표일 것이고
즉, 확률이 가장 높은 좌표값은
입력된 이미지들의 평균치에 해당하는 값을 가지는 이미지 벡터의 위치일 것이다.
이 값을 이용해 확률 분포를 만들어 낼 수 있을 것이다. ( 등장 빈도수가 높을 수록 높은 확률 )
확률 분포에 따른 벡터 뽑기
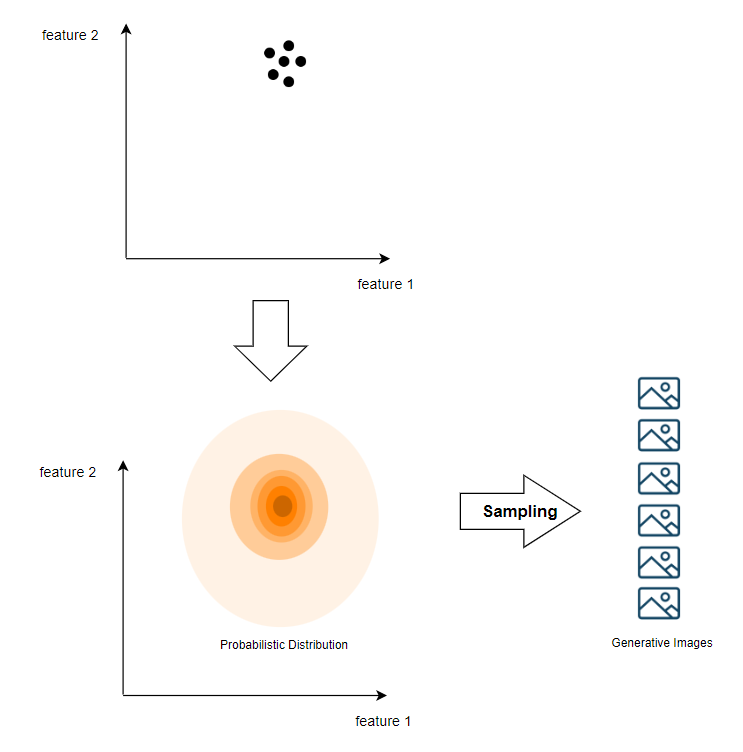
이제 이 확률분포에 따라 벡터를 뽑을 것이다.
그렇다면 입력으로 들어온 이미지들과 완전히 똑같지는 않지만
비슷한 성격을 지닌 이미지를 생성해 낼 수 있는 벡터를 뽑을 수 있다.
이 벡터를 가지고 다시 이미지로 만들어주면(다층 신경망을 이용) 완성이다.
지금까지 말한 내용은 이미지를 벡터 공간에 위치시킬 수 있고
입력된 이미지들의 특징들을 골고루 담고 있는 이미지를 뽑기 위한 확률 분포를 얻을 수 있다는 것이다.
전반적인 모델 구조
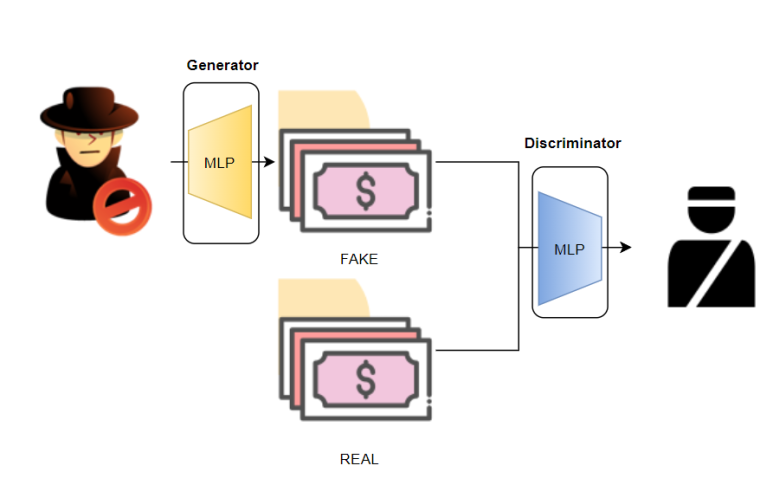
GAN 모델에는 총 2개의 MLP가 존재하며 학습된다.
| 위조범 입장에서 학습
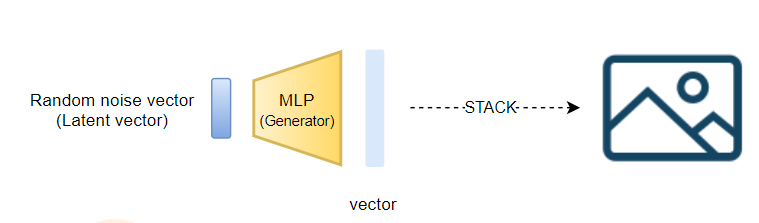
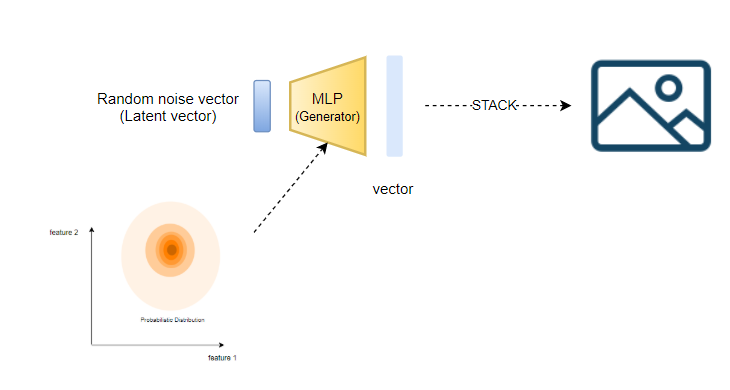
가장 먼저 이미지를 생성해내는 Generator의 경우
1. 랜덤 노이즈 값으로 만든 벡터를 MLP에 통과시킨다
2. 출력 벡터를 잘라서 쌓으면 이미지가 된다.
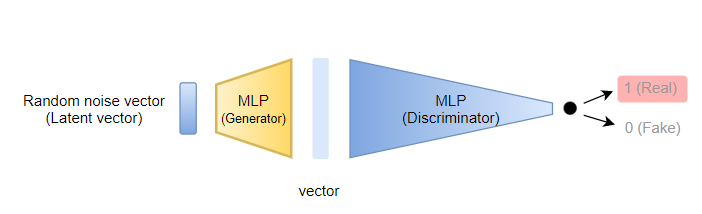
위조범 입장에서는 생성해낸 이미지가 진짜로 판단되기를 바라기 때문에
Discriminator에 해당하는 MLP의 output이 Real값을 나타내도록 학습시킨다.
여기서 Generator만 학습하기 위해
Discriminator MLP의 가중치는 고정된 상태로 가중치 업데이트를 진행한다.
| 경찰 입장에서 학습
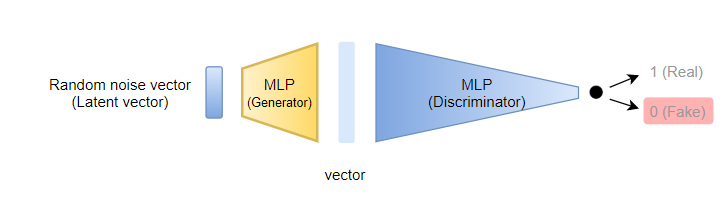
경찰 입장에서는 위조범이 만든 이미지가 가짜로 판단되기를 바라기 때문에
Discriminator에 해당하는 MLP의 output이 Fake를 나타내도록 학습시킨다.
추가적으로 실제 이미지는 진짜로 판단되기를 바라기 때문에
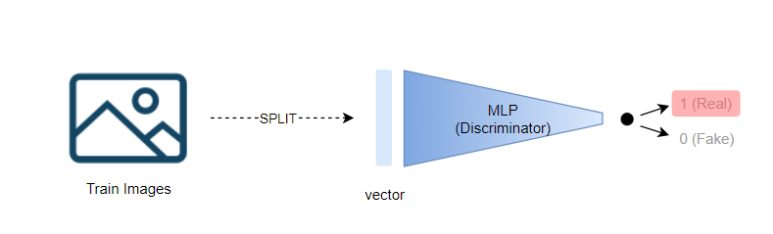
실제 이미지를 Discriminator에 넣었을 경우 MLP의 output이 Real을 나타내도록 한다.
경찰 입장에서는
가짜와 진짜를 구별하기 위해서
가짜를 구별할 수 있는 능력과, 진짜를 구별할 수 있는 능력을 함께 길러야 한다.
즉, 위의 두 MLP가 동시에 학습되어야 한다는 점이다.
그래서 두 MLP의 Loss를 각각 구한다음에
평균 낸 것을 Discrminator의 Loss로 정한다.
(물론 Discriminator를 학습 중일 때에는 Generator의 가중치는 고정시켜 준다.)
학습이 완료된다면,
Generator에 해당하는 MLP 속에는
학습에 사용된 이미지들과 비슷한 성격을 가진 이미지를 생성해낼 수 있는
확률 분포가 녹아 들어가게 된다.
이제 이 모델을 가지고 확률적 뽑기를 통한 특성 선택으로
새로운 이미지가 생성된다.
자세한 목적함수 설명
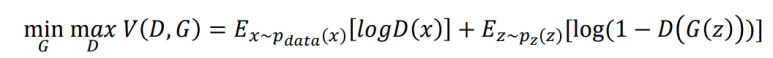
GAN의 목적함수는 위와 같은 minmax 이다.
즉, min을 하면서도 한편으로는 max를 한다는 뜻이다.
여기서
" Loss는 손실이므로 항상 줄여야 하지 않나 ? "
라고 생각할 수 있는데
목적함수(Object function)와 손실함수(Loss function)은 구분해야 한다.
목적함수는 모델이 우리가 원하는 방향으로 최적화하기 위해
최적 지향점이 존재하는 함수임과 동시에
특정 가중치의 Gradient 값을 구하는 도구이다.
그래서 우리가 원하는 결과를 내뱉기 위한
목적함수의 최적값이 있다면 그 최적값을 향해
위에서 아래로 내려가거나(min), 아래에서 위로 올라갈 수 있다(max).
이제 하나하나 살펴보자.

노이즈 벡터 z를 Generator에 통과시켰을 때의 출력값이다.
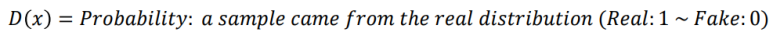
훈련 이미지 x를 Discriminator에 통과시켰을 때
진짜(Real)일 경우 1을 반환하고, 가짜(Fake)일 경우 0을 반환하는 출력값이다.
즉, 들어온 이미지 x가 진짜일 확률값을 나타낸다.
원본(학습) 데이터에 대한 부분
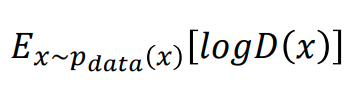
학습시키려는 진짜 이미지 x가 있을 텐데
이 x는 pdata라는 확률분포로 이루어져 있다. ( 앞서 설명한 이미지의 확률 분포를 의미한다 )
그래서 위의 값은
pdata라는 확률분포에서 x(원본 이미지)를 뽑고 => pdata(x)
이를 Discriminator에 통과시킨다음 log를 씌운 값( logD(x) )의
기대값이다.
생성 데이터에 대한 부분
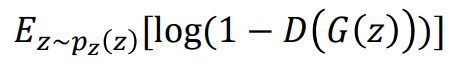
Generator의 입력으로 사용할 랜덤 노이즈 벡터 z는
pz라는 확률분포로 이루어져 있다.
그래서 위의 값은
pz라는 확률분포에서 z(랜덤 노이즈 벡터)를 뽑고 => pz(z)
이를 Discriminator에 통과시킨값에 음수를 취한다음 1을 더해주고 log값을 씌운 값( log(1-D(G(z)) )의
기대값이다.
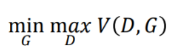
이제 이것의 의미를 확인해보면,
앞서 설명한 두 부분을 더한것을 V(D,G)라고 하고
G(Generator)를 업데이트 할 때에는 V(D,G)를 최소화(min)하는 방향으로 학습하고
D(Discriminator)를 업데이트 할 때에는 V(D,G)를 최대화(max)하는 방향으로 학습한다는 뜻이다.
왜 그런지 확인해보자.
G(Generator)를 업데이트 = 위조범 입장에서 학습
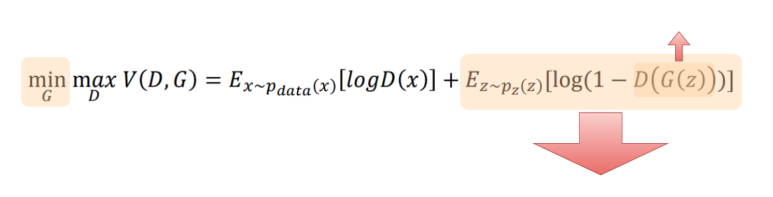
위조범 입장에서는 랜덤 노이즈 벡터 z를 Generator라는 MLP를 통과시켰을 때
그 이미지가 진짜(Real)로 판단되기를 원한다.
그렇다면 그 이미지에 해당하는 G(z)가 포함된 둘째 항 만 보면 되고
Discriminator가 진짜로 판단한다면 1을 내뱉어야 하므로
log 내의 값은 Discriminator가 진짜로 판단 할수록 작아지게 되고 ( log 내의 값은 0보다 크고 1보다 같거나 작다 )
그렇다면 log값은 작아지게 된다.
그러므로 둘째 항을 최소화 하는 방향으로 학습된다.
D(Discriminator)를 업데이트 = 경찰 입장에서 학습

경찰 입장에서는 실제 이미지는 진짜로 판단함과 동시에,
가짜 이미지는 가짜로 판단하기를 원한다.
그렇다면
첫번째 항에 진짜 이미지를 넣었을 경우 진짜로 판단할 수록 D는 1이 됨으로써 커지게 되고
두번째 항에 가짜 이미지( G(z) )를 넣었을 경우 log 안의 값이 커지게 됨으로써( log 내의 값은 0보다 크고 1보다 같거나 작다 ) 둘째 항도 커지게 된다.
즉, 모든 항을 최대화 하는 방향으로 학습된다.
+ 추가적으로 GAN의 여러 Loss Function
한계점
Mode collapse
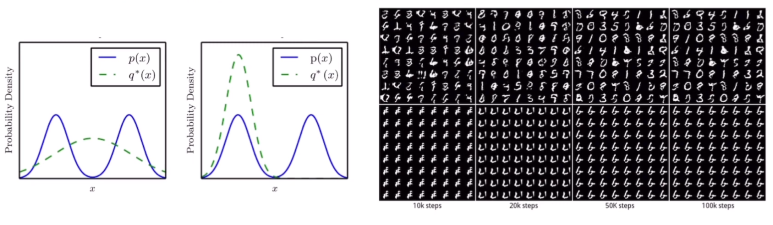
확률 분포의 형태를 전반적으로 맵핑(따라감)하기 보다는,
단순히 오류를 최소화하는 최빈값(mode)에만 집중하여 학습하게 되어
실제값(학습 이미지)들 중에 특정한 형태만 생성된다.
위의 그림은 p(x)가 실제값의 확률분포인데
optimal 확률 분포가 한쪽 최빈값에만 잘 출력이 되도록 구성이 되었다.
하지만 여기서 모델은 두개의 봉오리중 한 봉오리에 대한 출력값만 내놓아도 정답으로 판단하기 때문에
분포 전반을 아우르는 학습이 되지 않을 수 있다.
이를 보완하기 위해 mini-batch discrimination이나 feature matching등이 도입된다.
How to evaluate
사실 생성된 결과 이미지가 잘 생성된 것인지 판단 가능한 지표가 없다.
이에 따라 학습을 얼마나 진행해야 하는지에 대한 명확한 기준이 부족하다.
대부분 GAN의 성능 지표는 Inception Scroe라는 생성된 이미지의 다양성을 측정하는 지표를 사용한다.
Unstable training
앞선 목적함수를 보다싶이
한쪽은 낮추려고 하고, 한쪽은 높이려고 하는 minimax 게임을 통해 학습이 되게 되는데
이때, G와 D 간의 균형이 깨지기가 쉽다.
그래서 DCGAN등 학습을 안정적으로 바꾸고자 구조를 새로 제안하는 모델이 등장했다.
GAN의 파생들
- DCGAN : MLP가 아니라 CNN으로 GAN을 구축해서 이미지에 특화되고 안정적이다.
- cycleGAN : 이미지의 스타일을 다른 이미지로 변경하는 GAN이다. (낮-> 밤 등)
- WGAN : mode collapse를 해결하기 위해 BCE loss 대신에 wasserstein loss를 제안한다.
- DiscoGAN : 서로 다른 객체 그룹 사이의 특성을 파악해 합성 또는 변환이 가능하다. ( 신발+가방 => 가방 신발 )
( 말 -> 얼룩말 변환 )
- AnoGAN : 정상 데이터 생성자를 학습해 anomal를 판단
자세한 논문 리뷰(추가 예정)
MNIST 그림을 이용한 GAN 모델을 생성해보았다.

생성된 그림
생각보다 준수한 성능을 보여주는 것을 확인할 수 있다.
'Computer Vision' 카테고리의 다른 글
| [GAN 시리즈] StackGAN에 대한 모든 것 (논문 리뷰) (1) | 2023.02.05 |
|---|---|
| [GAN 시리즈] CGAN(Conditional Generative Adversarial Nets) 간단 정리 (0) | 2023.01.22 |