오늘은 정말 중요한 PCA와 SVD (특이값 분해)차원축소에 대해 다룰 것이다.
선형대수학을 배웠으면 천천히 따라가면서 충분히 이해 할 수 있을 것이다.
부디 이를 정확이 이해하고 싶다면 자신만의 언어로 만드는 시간을 들여 곱씹어 갔으면 좋겠다.
솔직히 개념만 단순히 들으면, 직관적인 이해보다는 때려넣기식으로 느낄 수 있다.
이번 정리는 눈에 보이도록 하여 직관적인 이해를 가능하게 할 것이다.
가장먼저 PCA를 설명하겠다. SVD는 더 간단하므로 PCA를 이해하고 나면 껌으로 보인다.
PCA
PCA를 설명하기 전에 차원축소에도 종류가 있다.
1. Feature extraction과 2. Feature selection으로 나뉜다.
Feature extraction은 모든 feature들을 가장 잘 타내는 더 작은 차원들의 feature를 찾는 것이다.
즉, 원래 정보를 최대한 보존하여 적은 차원에 나타내겠다는 것이다(차원축소의 목적 : 계산 단순화)
Feature selection은 모든 feature들의 공통된 부분들을 없에 feature들간의 차이점을 키우는 것이다.
(SIF에서 마지막에 했던 것이다.)
그러므로 PCA는 Feature extraction이다.
PCA 설명을 시작하겠다.
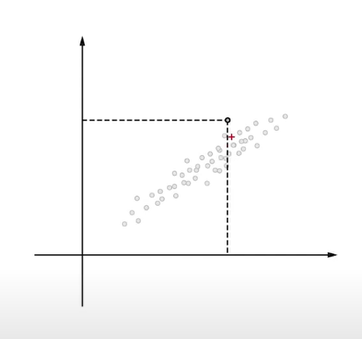
2차원에 다음과 같은 분포로 정보들이 위치한다고 치자.
우리는 계산을 간단하게 하기 위해 저 정보들을 1차원으로 표현하고 싶다.
그렇다면, 어떠한 축(벡터)을 잡아야 할까?
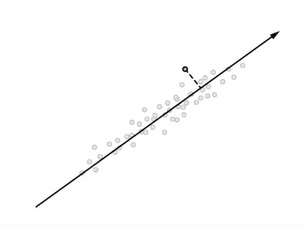
바로 다음 방향의 축일것이다.
저 축이여야지만, 모든 정보들간의 차이점을 적은 차원에서도 효과적으로 나타낼 수 있다.
이 말은 즉슨, 적은 차원에서도 정보가 잘 보존되려면 모든 정보들을 새로운 축에 사영시켰을 때
최대한 서로 많이 흩뜨려놓아야(분산이 높아야)한다는 것이다.
만약

다음과 같이 빨간축을 잡았다면 어떻게 될까?
모든 정보의 차이점이 아까보다 좁은 주황색 영역으로만 표현된다.
이는 정보간의 차이점을 효과적으로 보여주지 못한다.
그러므로 우리는 정보의 분산이 가장 큰 축을 찾아야 한다.
그리고 이축을 이용해 최종적으로,
축을 기준으로 정보들을 표현해야 한다.(원래 기존 2차원이 아닌, 1차원상에서 표현해야 한다.)
+ 더 직관적인 그림

저 보라색 선(축, 벡터)를 찾아 사영시키고, 그 축의 중심을 기준으로 얼마나 떨어져 있느냐에 따라 정보에 값을 부여하는 것이다.(1차원적)
정보의 분산이 가장 큰 축은 어떻게 찾을까?
이는 선형대수학을 공부하였다면 해결 가능하다.
이때 필요한 지식들을 복습하는 겸 잘 정리해놓은 사이트를 소개하겠다.
[선형대수학 #3] 고유값과 고유벡터 (eigenvalue & eigenvector)
선형대수학에서 고유값(eigenvalue)과 고유벡터(eigenvector)가 중요하다고 하는데 왜 그런 것인지 개인적으로도 참 궁금합니다. 고유값, 고유벡터에 대한 수학적 정의 말고 이런 것들이 왜 나왔고 그
darkpgmr.tistory.com
축을 구하는 과정은 바로 고윳값과 고유벡터를 구하는 과정이다.
선형대수학을 공부한 사람이라면 SVD나 PCA의 식을 딱 보면, 대각화와 선형변환(회전변환 등)이 떠오를 것이다.
가장 먼저 재미있는 선형대 기저변환 관련한 내용을 설명하겠다.

다음과 같은 타원이 있다. 하지만 어딘가가 불편하다. 2cxy라는 부분이 더해져있다.
저 타원의 넓이를 어떻게 구할까?
기본적인 타원이라면
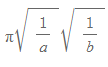
하면 끝이지만 저 경우는 불가능하다. 타원이 원점을 중심으로 회전한 상태이기 때문이다.
이를 바꿔볼 수 는 없을까?

축을 기존의 x,y에서 빨간색 x',y' 축으로 변경한 다음에
x',y'축에 대하여 타원을 나타낸다면 아까 공식을 이용해서 넓이를 쉽게 할 수 있다.
이때 우리는 저 축 변경을 고윳값과 고유벡터를 통해 해결 할 수 있다.

원래 좌표의 타원식은 다음과 같이 행렬3개의 곱으로 나타낼 수 있다.

그리고 그때 가운데 끼인 행렬 A의 고윳값을 가지고 우리는 놀라운 일을 할 수 있다.

고윳값만 안다면, 우리는 새로운 축에 대한 타원 식을 구할 수 있다. 이것이 가능한 이유는 회전행렬에 대한 깊은 이해가 있으면 가능하다.
관련 내용은 다음 링크를 참고하면 된다.
https://m.blog.naver.com/gt7461/221033990289
회전변환 타원
[그림1] 타원 (1)에서 r>0이면 주축(장축)의 기울기의 부호는 반대로 마이너스(-), r<0이면 주축의 ...
blog.naver.com
https://studyingrabbit.tistory.com/6
[선형대수-2] 이차형식과 행렬 대각화 : 고유값에 따른 타원곡선의 결정
이번 포스팅에서는 행렬의 대각화가 이차형식에 대해 이해하는데 어떻게 활용 될 수 있는지를 알아보겠습니다. 행렬의 대각화를 이용해 복잡한 것을 단순하게 이해하는 가장 기본적인 예시라
studyingrabbit.tistory.com
그렇다면 저 새로운 축에 대한 타원식도 행렬로 나타내는 것이 가능하다.

어딘가 특이값 분해와 아주 유사하다. 사실 똑같다. 이를 나중에 직관적 이해에 활용할 것이다.
이제 PCA의 과정을 살펴보자.
PCA를 하려면 분산을 최대화하는 축을 찾을것이므로 분산을 먼저 구해야 한다.
이때 X와Y가 얼마나 흩어졌는지 상관관계를 나타내는 공분산을 이용한다. (그냥 분산을 이용하기도 함)
공분산의 정의는 다음과 같고

다음과 같은 성질을 띈다.

이를 이용해 어떠한 뱡향으로 분산되어있는지를 행렬로 나타내는 것이 가능하고,
이 여려 방향들을 참고하여 최종적으로 가장 넓게 퍼져있는 방향을 찾는 것이다.

이를 행렬로 나타내면 다음과 같다.

그리고 이 행렬을 고윳값 분해한다. (공분산 행렬이 대칭행렬이여서 대각화 가능)

이때 ei들은 고유벡터로 모두 수직이여서 독립이다
=> 이 독립에 대해서 자세히 이야기 하면 다음과 같다.
우리가 좌표축 x,y를 이용할 때, x,y는 왜 수직일까?
그 이유는 다음과 같다.
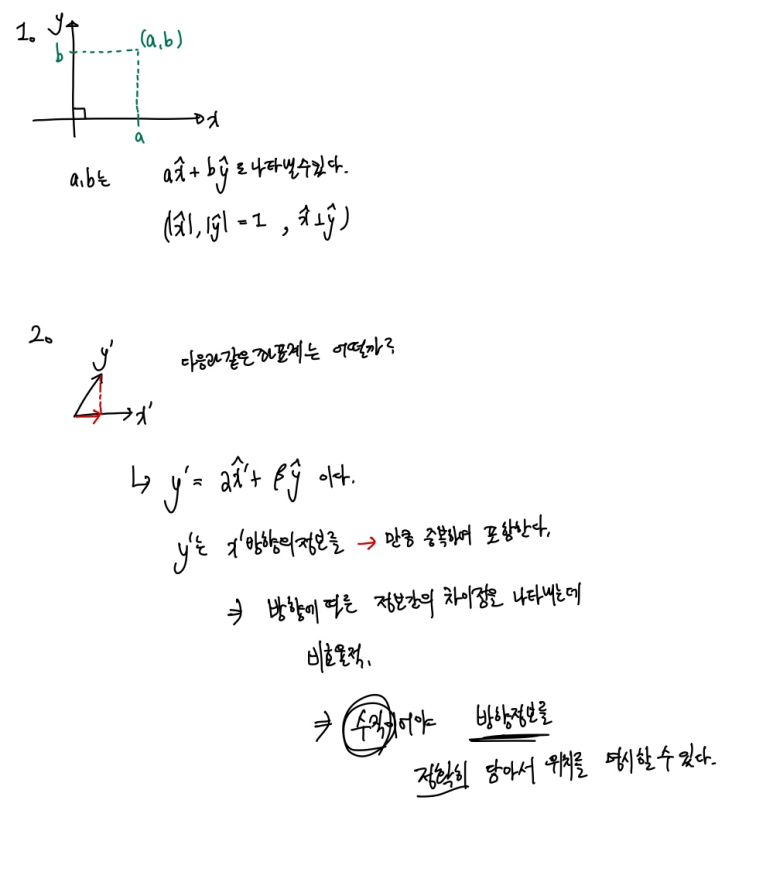
수직이 아니면, 한 방향의 정보가 다른 방향의 정보의 일부를 포함해버려서
방향에 따른 정보의 경향성을 정확히 파악하지 못한다.
이제 저 위의 식을 뜯어보면,
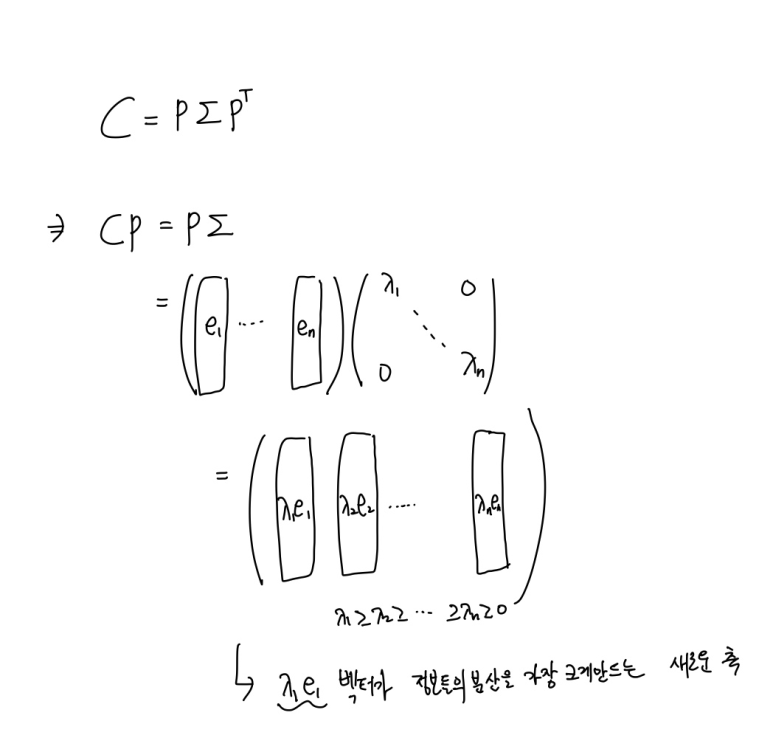
다음과 같다. 어디선가 본듯하다. 아까 타원이랑 비교해보자.

타원에서 고윳값이 각 축에 따른 타원의 펑퍼짐한 정보를 담고 있듯이,
우리는 공분산을 분해해서 구한 고윳값이 새로운 축에 따른 정보들의 분산정도(펑퍼짐)를 가짐을 직관적으로 이해 할 수 있다.
이 공분산 행렬의 고유벡터들이 새로운 축이 되는 것에 대한 수식적 증명은 다음 사이트에서 확인 가능하고 전체적인 활용에 대한 설명도 완벽하게 해놓았다. 정말 대단한 사이트이다.
우리는 이렇게 공분산을 대각화 하여 고윳값을 찾고
각 고유값에 따른 고유벡터들이 새로운 축이 됨을 알 수 있다.
이후 e1, e2 ... 들 중에 뒤에 부분 몇개의 열벡터를 죽여서 차원을 축소한다. (en,en-1, 등등) 이들은 고윳값이 작아 정보들의 분산이 크지 않는 축이다.
직관적으로 이해하면, 원래 좌표축에 따른 n차원(좌표축이 n개이다)에서의 정보들의 공간상 좌표들을,
정보들의 분산을 고려하여(어느쪽으로 펑퍼짐하거나, 뾰족하거나 한 정도를 고려)
원래의 정보들을 새로운 좌표축에 따른 n차원으로 표현한다.
이후 고윳값이 작은 고유벡터 축(분산이 작은 => 정보들의 차이를 구분하기 힘든 축으로 정보를 나타낸 부분)
을 몇 개 제거하여 더 적은 k(k<n)차원 (좌표축이 k개)로 표현하여 차원 축소가 가능해진다.
=> 우리는 정보들의 차이를 구분하기 쉬운(분산이 큰) 축들은 죽이지 않고 좌표계로 삼고 그 좌표계에 따른 기존의 정보들을 표현했으므로 정보의 차원을 축소하였지만 손실을 최소화했다고 볼 수 있다.
이때 공분산을 사용하지 않고 분산을 사용하는 방법은

다음과 같고
열의 평균을 0이라 하는 부분에서 평균으로부터 얼마나 떨어져 있는지를 행렬에 담아 분산을 표현한다.
이 부분에 대한 설명은 다음에서 이해 할 수 있다.
주성분 분석
[일반인을 위한] K-MOOC 인공지능을 위한 기초수학 입문 (Introductory Mathematics for Artificial Intelligence) 이상구 with 이재화, 함윤미, 박경은 V. 주
matrix.skku.ac.kr
마지막으로 저래 구한 행렬 CP를 어떻게 이용을 하는가?
단순히 원래 정보에 저 새로운 축들(고유벡터들)과 각각 내적하고 모두(고유벡터 갯수만큼 = 원하는 차원수만큼) 더하면된다.
하지만 다른 방법으로 하나의 행렬로 만드는 것도 가능하다.
선형대수학에 나오는
선형사상의 사상행렬을 떠올리면 된다.
사상행렬을 급하게 배운 사람이면(대학교 편입에서는 이를 기계적으로 외운다) 이 행렬의 엄청난 포텐셜을 놓쳤을 가능성이 높다. 하지만 다음을 이해한다면 이 행렬을 보면 차원과 차원과의 이동이 거시적으로 보일 것이다.
선형 사상을 간단히 소개하겠다. (내 전공과목 책인 Introduction to Robotics(John J. Craig)은 이 사상을 현실에 직접적으로 사용하는 방법을 소개하므로 필요한 사람은 구글링을 통해 무료로 받을 수 있다.)

선형사상 행렬은 한 정보에 대한 두 좌표계간의 표현임을 정확이 인지해야 한다.
그리고
X' 이 A에 X를 곱해줌으로써 X 좌표계(차원)에서 표현된 한 점의 위치를 X'에서 표현된 점의 위치로 변환 하는 것이 가능한 이유를 A에서 찾아내야 한다.

기존의 X좌표계에서 (1,0,0,...,0)을 넣으면 어떻게 될까?
그러면 행렬 A의 1번열만 살아남아 X'이 될 것이다.
그렇다면 우리는 X좌표계의 기본 기저(축)인 x방향 유닛벡터 (1,0,0,...,0)이 X'에서는 X'벡터로 나타남을 알 수 가 있다.
이를 정리해보자

그렇다면 이제 X부분에 X좌표계로 표현한 값을 넣기만 하면, 각 기저에 각 기저에 알맞는 스칼라 값(길이값)이 곱해쳐서 새로운 좌표계에서 표현된다.

기저변환 행렬 구하는 과정은 다음에서 이해 가능하다.
https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=ldj1725&logNo=221229190412
[2.77] 기저에 대한 좌표와 기저변환
어떤 한 기저가 있다고 합시다. 그 기저는 어떤 목적에서는 유용할 수 있습니다. 그러나 목적이 달라지면 ...
blog.naver.com
위 링크에서는 2차원만 다루지만 다차원도 가능하다(다변수 방정식 해푸는것이므로 단순하다(컴퓨터에게))
이제 기저변환 행렬을 구하면 원래 좌표계의 정보들을 집어넣어 새로운 좌표계에서 의 위치들을 얻을 수 있고 이를 활용 가능하다.
SVD
이제 특이값 분해에 따른 차원축소를 보자. 이는 너무나도 쉽다.

그냥 원본행렬 X를 3개의 행렬로 분해한 다음에 U의 열과 VT의 행을 일부 짤라버리는 것이다. 하지만 시그마가 큰 부분을 포함하여 정보의 손실을 줄였음을 알 수 있다. 시그마는 왼쪽 위가 가장크고 오른쪽 아래로 내려갈수록 작다.
'Tensorflow 2 NLP(자연어처리) > 문장 임베딩' 카테고리의 다른 글
| [4-5] 잠재 디리클레 할당(LDA, Latent Dirichlet Allocation)이란? + 베이즈 정리,깁스 샘플링 (0) | 2021.11.13 |
|---|---|
| [4-4] Word2Vec에서 Doc2Vec까지 (0) | 2021.11.13 |
| [4-3] 잠재 의미 분석(LSA), TF-IDF를 이용한 문서 임베딩 (0) | 2021.11.13 |
| [4-1] 가중 임베딩, SIF(Smooth Inverse Frequency)란? (0) | 2021.11.13 |