Glove는 당시 Word2Vec과 잠재의미분석 두 기법의 단점을 극복하고자 나온 단어 임베딩 기법이다.
각각의 단점은 다음과 같다.
1. Word2Vec은 단어 간 유사도측정이 LSA(잠재의미분석)보다 유리하지만
사용자가 지정한 윈도우(타깃 단어 주위로 몇개의 단어까지 주변단어인가) 내의 로컬 문맥(local context)만
학습하기 때문에 말뭉치 전체의 통계 정보는 반영되기 어렵다.
(그러나 이 단점은 Levy&Goldberg 2014 에서 Skip-gram 모델이 말뭉치 전체의 글로벌한 통계량인
SPMI 행렬을 분해하는 것과 동치라는 점을 증명하여 사라졌다.)
2. 잠재의미분석은 말뭉치 전체의 통계량을 모두 활용할 수 있지만 단어간 유사도를 측정하기 어렵다.
이 단점을 극복하기 위해
Pennington et al. (2014) 논문
에서
'임베딩 된 두 단어 벡터의 내적이 말뭉치 전체에 대한 두 단어의 동시 등장 빈도의 로그 값이 되도록'
비용 함수를 정의했다.
이렇게 되면 임베딩 된 단어 벡터간 유사도 측정과 말뭉치 전체 통계 정보를 둘다 반영 가능하다.
간단한 정리와 엄밀한 정리로 나누어 설명하겠다.
간단히 정리하면
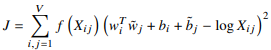
wiT 는 중심단어 i의 행벡터, wj는 주변단어 j의 열벡터이다.
bi,bj 는 계산상에 발생하는 문제를 없애주기 위한 편향(bias)항 이다.
f(Xij)는 가중치 함수로 행렬 X의 75~95%의 원소가 0인 것을 해결하기 위해 넣은 가중치 함수이다.
그래서 간단히 보자면, wiT wj 의 내적을 통해 코사인 유사도(단어 간 유사도)를 취하고
=> 그 값이 말뭉치 전체에서의 동시 등장 빈도의 로그값(logXij)과 유사해지도록 두 값을 빼고,
=> 편미분을 통해 J의 최솟값을 만들도록 하는
=> 중심단어와 주변단어의 벡터를 업데이트 하여 단어 임베딩을 하는 것이다.
엄밀하게 정리하면 다음과 같다.
가장 먼저 이해를 위한 단어 벡터 기초를 설명한 부분을 추가하겠다. (필요한 사람만)
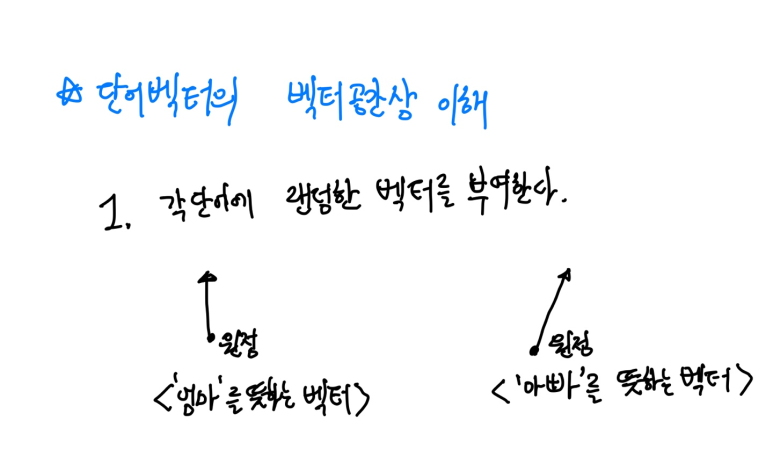
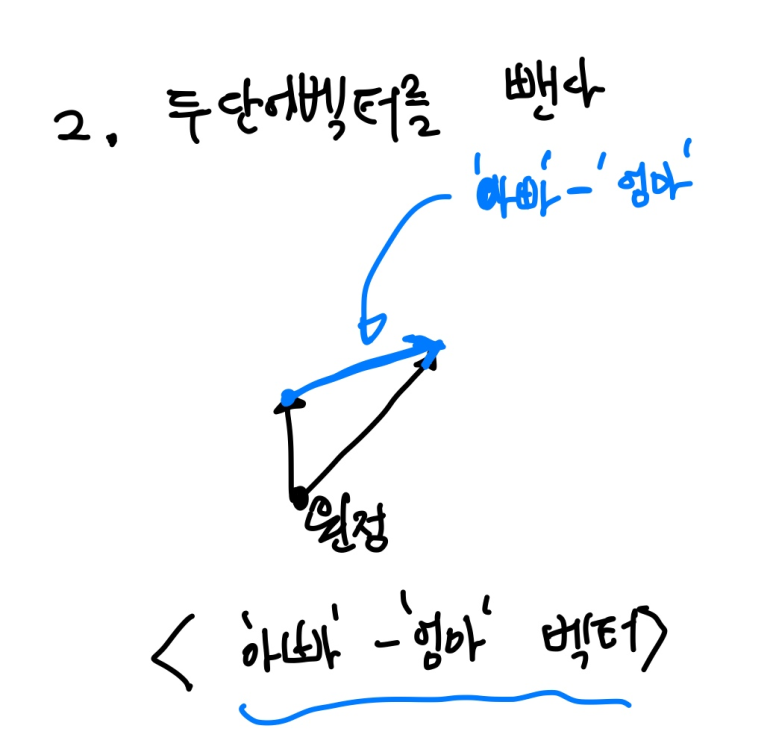


기초는 다음과 같다.
또한 우리는 단어 임베딩을 할 때
유사한 단어는 비슷한 방향을 보는 경향을 벡터에 부여하여 단어 유사를 타나낸다.
이때 두 단어 벡터 내적을 하게 된다면 유사할 수록 값이 클 것이고 이를 이용한 것이 코사인 유사도이다.
가장 먼저 흐름을 통해 정리하고 그 과정을 자세히 설명하겠다.
[ 전체적인 흐름 ]
1. 단어 임베딩에서 가장 중요한 모든 단어 간 관계를 잘 표현하고,
타깃 단어와 그 주변단어의 관계가 잘 표현되어야 한다.
2. 그러하도록 만드는 함수를 만들어 보자
3. 함수를 만들었으면 그 함수에서 잘 작동되고 있는 벡터(=임베딩 완료된 단어 벡터)를 찾고
그 벡터를 잘 정제하여(손실함수 줄이기) 단어 벡터를 뽑아내자.
[ 상세한 과정 ]
이제 논문 내용을 차근히 풀어보겠다.
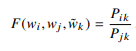
F가 앞서 말한 함수이다.
Pik는 조건부 확률로 중심 단어 i가 등장하였을 때, 주변단어 k가 같이 등장할 확률 이다. Pjk도 같은 유형이다.
Pik를 Pjk로 나눔으로써 두 확률간의 유사도를 스칼라로 표현 해놓았다.
어떠한 함수에 중심단어 2개 ,주변단어를 넣어주면 그 단어들간의 관계를 함축하는 값이 확률로 표현될까?
이때
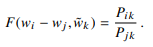
변수에 모든 단어 벡터를 따로 집어넣는 것이 아닌 서로 다른 중심단어 두 개는 서로 빼서 하나의 벡터로 만든다.
이러면 두 중심단어 간의 관계가 뺌으로 인해 하나의 벡터에 함축되게 된다. (앞서 말한 기초 참고)
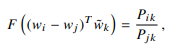
그런데 문제가 있다. 독립변수가 벡터인데 종속변수가 스칼라(확률)이다.
이러면 우리가 원하는 선형구조(간단히 요약해 응용 가능한 일반적인 구조)를 만들지 못한다.
그럼 독립변수를 스칼라로 만들어 주자. 그러기 위해 벡터 내적을 한다.
내적을 해도 각 벡터가 담고 있는 정보는 사라지지 않는다.
왜냐하면 내적 값을 통해 벡터간 유사도의 정보를 담을 수 있기 때문이다.
이 정보는 함수에 넣으면 우리가 원하는 결과 값을 얻을만큼 충분히 의미있는 정보이다.
이 식에서 만족해야 할 성질이 하나 있다. 바로 '준동형 homomorphism' 이다.
준동형의 정의는 다음과 같다.

간단히, 두 구조 A,B사이의 연산 및 관계가 보존되는 형태라고 보면 된다.
그러하다면 다음 등식을 만족한다.
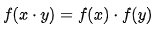
이것이 왜 나왔는지 살펴보면,
타깃단어가 있고, 중심단어가 있다.
중심단어에서 주변단어를 택하는 연산과정 (A) 과 주변단어에서 중심단어를 택하는 연산과정(B) 는
순서의 차이만 있을 뿐 동일한 과정이다. 순서가 바뀌어도 두 관계가 보존이 된다.
그래서 위의 등식을 만족 할 것이다. (등식 내의 '·' 는 이항연산(=두 항간의 이어지는 연산))
준동형을 만족하여 좌변의 식이 다음과 같이 표현 가능해진다.
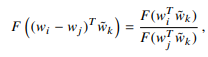
다음을 만족하는 F는 무엇일까? 'e' 임을 알 수 있다.
이제 식에서 잘 작동되고 있는 부분을 떼와서 손실함수 식을 만들어보자
일단,
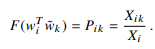
을 만족하니까 이제 e를 없에주기 위해 양변에 자연로그를 취해주자.
Xik는 중심단어 i 주위에 k가 등장한 횟수
Xi는 동시등장 행렬에서 i에 해당되는 행의 값을 모두 더한 값이다.
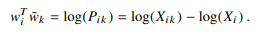
자연로그를 취하면 다음 식을 만족한다. 하지만 준동형을 만족하니까 i와k는 서로 자리를 바꿀수가 있는데
log(Xi)가 방해를 한다. 이를 없애주기 위해 편향(bias) bi를 추가한다. ( k가 독립이기 때문에 가능)
하지만 bi만으로는 교환대칭(i와k를 바꾸고도 대칭이 이루어 지도록)이 성립하지 않으므로
wk를 위한 bk를 더해주면 다음 등식을 얻을 수 있다.
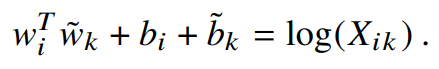
하지만 이것만으로는 충분하지 못하다. Xik에 해당하는 값이 0이 될 확률이 75~95%이기 때문이다. 그렇다면 -∞로 발산하므로 이를 해결하기 위해 어느 정도의 가중치를 부여한다.
이제 비용 함수 완성이다.
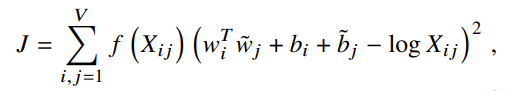
glove 비용함수
그리고 가중치 함수는 다음 성질을 따른다.

이때 Xij가 0인 경우에도 f(x)가 더 빨리 0으로 수렴해 최종적으로 손실함수가 수렴하게 만드는것이 가능해진다.
+플러스 가중치 함수의 엄밀한 정의
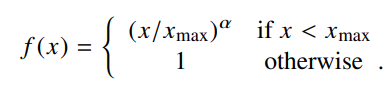
가중치 함수
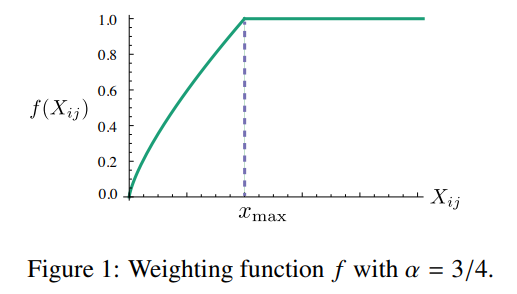
가중치 함수 그래프
가중치 함수의 a는 3/4 와 1인 경우가 선형 형태에서 가장 modest하다고 한다.
'Tensorflow 2 NLP(자연어처리) > 단어 임베딩' 카테고리의 다른 글
| [3-8] Swivel이란? (0) | 2021.11.13 |
|---|---|
| [3-7] PMI 행렬 만드는 법 (0) | 2021.11.13 |
| [3-5] Matrix Factorization이란? (0) | 2021.11.13 |
| [3-4] 잠재 의미 분석(LSA,Latent Semantic Analysis) 이란? (0) | 2021.11.13 |
| [3-3] FastText란? (0) | 2021.11.13 |