keras의 layers 클래스의 dot 메소드의 구조에 대해 알아보자.
처음 봤을 때에는 바로 계산 방식이 보이지 않았지만
코드를 통해 결과를 보면서 이해를 한 것을 정리한다.
일단 공식 홈페이지는 다음과 같이 간단히 설명한다.
https://www.tensorflow.org/api_docs/python/tf/keras/layers/Dot
tf.keras.layers.Dot | TensorFlow v2.10.0
Layer that computes a dot product between samples in two tensors.
www.tensorflow.org
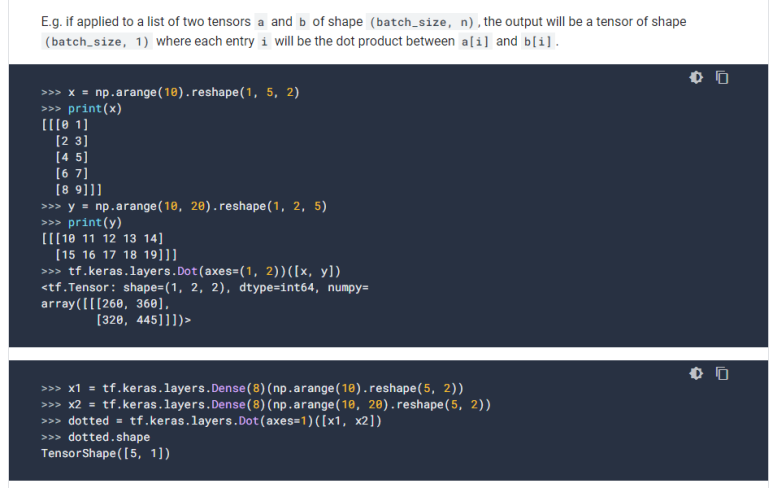

바로 한눈에 이해하기는 힘들다...
그리고 내가 보았던 코드는

저 axes=-1 이라고 되어있고, 이는 공식 API에서는 확인해볼 수 없었다.
그래서 기존의 axis의 표현 방법을 다시 정확하게 이해하고 정리해야 했다.

시각화 하면 다음과 같다.

이미지를 통한 이해를 위해, 벡터 하나하나의 계산 방식을 고려해서 시각화 해보았다.
그때 사용한 코드는 다음 레포지토리에 담겨있다.
https://github.com/DonghaeSuh/NLP_tensorflow2/blob/main/0_Test/keras.layers_test/layer_dot().ipynb
GitHub - DonghaeSuh/NLP_tensorflow2
Contribute to DonghaeSuh/NLP_tensorflow2 development by creating an account on GitHub.
github.com
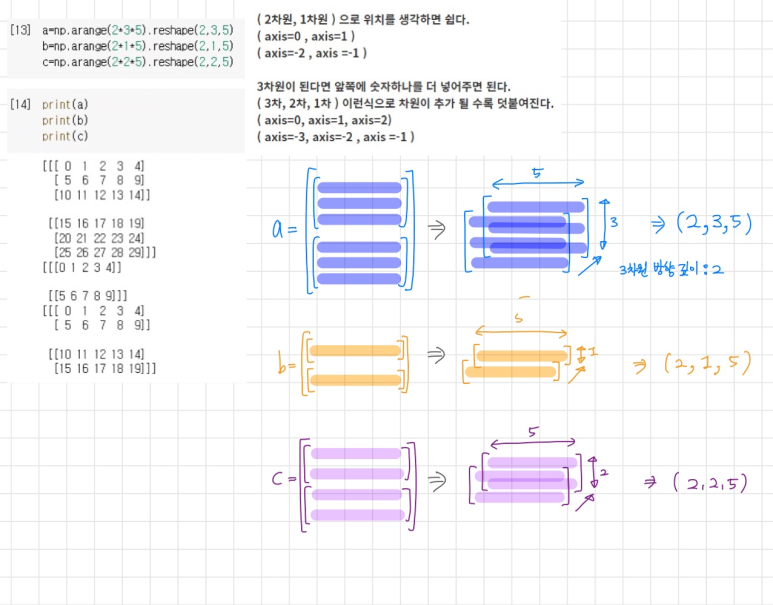
가장 먼저 3차원 a,b,c 행렬을 만들어 보았다.
『 dot ( [a,b] , axes = -1 ) 』
axes=-1은 axes=2(1차원 행방향) 이라는 것을 확인하고,
1차원 행방향에 대해 내적을 한다고 한다.
하지만 a,b 모두 3차원이므로 행렬 내적을 할 때에는 a,b의 각 샘플(2차원 행렬)끼리 계산을 할 것이다.
즉, 3차원 행렬은 다음과 같이 표현 할 수 있다.
=> (samples, row 갯수, column 갯수)
이때 a,b의 샘플의 갯수는 같아야 한다(3차원 깊이가 동일해야 한다.)
그리고 GPU는 병렬 연산이 가능하므로,
a와 b의 같은 깊이의 샘플끼리 연산을 한번에 수행하므로써(3차원 index가 같은 2차원 행렬끼리 연산)
깊이가 몇이 되든(샘플의 갯수가 몇개가 되든) 수행 시간은 동일하게 된다.

일단 기본으로 위의 내용을 확인해두고,
샘플 1개만 자세히 보자.(나머지 샘플들의 계산 방법은 동일하다)
dot([a,b], axes=-1)
을 한다는 것은 샘플 안에서
1. [a,b] : a에서 b를 참조해서 계산한다.
2. axes=-1 : 행방향 벡터를 기준으로 내적한다.
라는 뜻이다.
그리고 모든 행렬 곱이 그렇듯이 다음 규칙을 따른다.

이것이 정확히 무엇인지를 이미지를 보며 이해해보자.

가장먼저
a,b의 shape를 확인하면
a = (2,3,5)
b = (2,1,5)
이다.
연산 조건을 확인해보면
1. 일단 sample의 갯수가 2개로 같으므로 ok,
2. 그리고 각각의 행벡터를 내적을 할 것이므로 두 a,b의 column의 갯수가 5로 동일하므로 ok
(벡터 내적 :각각의 원소끼리 곱)
그렇다면 연산이 가능하다.
이제 샘플 1을 자세히 보면,
1벡터와 4벡터를 내적한다.
그리고 1벡터 연산이 끝났으므로 다음 행으로 넘어간다.
(a에서 하나의 벡터를 가지고 연산이 끝났으므로 출력이 다음 행으로 넘어간다)
이제 2벡터, 3벡터에 대해서도 각가 4벡터와 내적을 한다. 당연히 출력이 다음 행으로 넘어간다는 것을 볼 수 있다.
이 계산방법은 모든 sample들에서 동일하게 이루어지고, 병렬연산되어 한꺼번에 연산된다.
다른 예제를 통해 아까의 문장을 다시 확인해보자.


이것도 1개의 샘플을 먼저 보자.
dot([a,c], axes=-1)가 되어서 b가 c로 바뀌었다.
shape를 보면,
a = (2,3,5)
c = (2,2,5)
그리고 연산 가능한지 확인
1. 일단 sample의 갯수가 2개로 같으므로 ok,
2. 그리고 각각의 행벡터를 내적을 할 것이므로 두 a,b의 column의 갯수가 5로 동일하므로 ok
(벡터 내적 :각각의 원소끼리 곱)
연산 가능!
하지만 계산을 할때,
1벡터를 가지고 4벡터와 내적을 한 후 5벡터와도 내적을 해야한다.
(이는 a의 하나의 벡터를 가지고(1벡터) b의 하나의 벡터에 대한 연산(내적)이 끝나서(4벡터)
=> 출력이 다음 열방향으로 넘어가서 1벡터와 5벡터의 내적이 2번째 열에 적힌다.
이후 2벡터와 4,5벡터 / 3벡터와 4,5벡터의 내적이 규칙에 맞게 적힌 후
모든 샘플에 대해 동일하고 한꺼번에 연산된다.
이제 대망의 axes=(1,2)란 무엇인가..?
『 dot ( [x, y] , axes = (1, 2) ) 』
일단 아까 알았던 사실중
1. [x,y] : x에서 y를 참조해서 계산한다.
에 더하여
2. axes=(1,2) <=> axes(-2,-1)
: x의 axis=1(2차원 방향 : 열방향) 벡터를 가지고, y의 axis=2(1차원 방향 : 행방향) 벡터와 계산
이라는 새로운 규칙이 추가된다.
이것도 이미지로 보자.
그리고 아까 규칙도 또 다시 보자.


일단 x,y의 shape부터 보자.
1. x = (2,3,2)
2. y = (2,2,3)
연산 조건을 확인해보자.
1. 일단 sample의 갯수가 2개로 같으므로 ok,
아까와는 다르게 다른 조건이 생긴다.
2. x의 row 갯수와 y의 column 갯수가 같아야한다. ok ( 3 = 3 )
( 벡터 내적을 하려면, 두 벡터의 차원(원소의 갯수)가 같아야 한다.)
=> 즉, x,y의 2차원,1차원 값이 서로 교차되면 된다. x = (3,2) <=> y = (2,3)
1,2 를 모두 만족하므로 연산 가능하다!
x의 열벡터에 대해 y의 행벡터들과 내적을 하는 것이기에
1벡터에 대해 3벡터를 내적한 이후, 4벡터도 내적한다.
이것은 하나의 x에 대해 y에서 다음 계산으로 넘어가면 출력이 다음 열로 넘어가는 것이므로 확인해주자.
x에서 1벡터에 대한 연산이 끝났으므로, 출력이 다음 행으로 넘어가서
2벡터에 대해서도 3벡터,4벡터를 각각 내적해준다.
이는 모든 sample에 대해 같은 방식으로 동시예 계산된다.
마지막으로 생각해야 할 것이 있다.
axes=(1,2) 가 있다면, axes=(2,1) 도 있지 않을까?
조건만 된다면 가능하다!
『 dot ( [x, y] , axes = (2, 1) ) 』

일단 x,y의 shape부터 보자.
1. x = (2,3,2)
2. y = (2,2,3)
아까랑 동일하다.
연산 조건을 확인해보자.
1. 일단 sample의 갯수가 2개로 같으므로 ok,
2. x의 column 갯수와 y의 row 갯수가 같아야한다. ok ( 2 = 2)
( 벡터 내적을 하려면, 두 벡터의 차원(원소의 갯수)가 같아야 한다.)
=> 즉, x,y의 2차원,1차원 값이 서로 교차되면 된다. x = (3,2) <=> y = (2,3)
1,2 를 모두 만족하므로 연산 가능하다!
x의 행벡터에 대해 y의 열벡터들과 내적을 하는 것이기에
1벡터에 대해 3벡터를 내적한 이후, 5벡터, 6벡터도 내적한다.
이것은 하나의 x에 대해 y에서 다음 계산으로 넘어가면 출력이 다음 열로 넘어가는 것이므로 확인해주자.
(y에서 3번 계산하므로 3개의 열이 생겼다)
x에서 1벡터에 대한 연산이 끝났으므로, 출력이 다음 행으로 넘어가서
2벡터에 대해서도 3벡터,4벡터,5벡터를 각각 내적해준다.
3벡터도 마찬가지..
이는 모든 sample에 대해 같은 방식으로 동시에(병렬처리) 계산된다.
이 행렬 내적에 대한 연산은 자연어 처리에서 attention을 구하는데 사용 될 수 있으므로,
정확히 이해해야 해서 자세하게 정리해 보았다.