Decision Tree
: 머신러닝의 분류,예측 알고리즘중 하나.
<장점>
1. 결과의 원인 분석이 쉽다.
2. 간단하다.
3. 빠르다.
<구조>

1. Root node : 나무의 가장 꼭대기
2. Splitting(branch) : node의 출력
3. Decision node(internal node) : 하나의 특성(attribute,class)
4. Leaf node(terminal node) : 마지막 node
<기본 알고리즘>
1.ID3(하나의 Decision node에 대해 3개 이상의 branch(가지) 생성 가능
=> ID3 알고리즘을 보완하여 C4.5가 개발되었고, C4.5를 보완하여 C5.0이 개발됨
: Information gain을 이용하여 판단
2. CART (하나의 Decision node에 대해 2개의 branch(가지) 생성
: Gini impurity를 이용하여 판단
<< 생각해야 할 것 >>
1. 최대한, 분기(branch)를 나눌 때,
class 간의 구분이 명확하게 만든다.(같은 class 끼리 잘 분리되도록 하는 Decision 선택)
2. 언제 Decision을 멈출 것인가?
<엔트로피 (Entropy)>
엔트로피(Entropy)
: 샘플들의 집합의 불순도를 측정할 때 기준이 되는 척도
집합 S에 대해, 엔트로피는 다음과 같이 정의된다.

예를들어
1. S=25개의 샘플, 15개는 positive, 10개는 negative
=> S의 엔트로피

2. 모든 샘플이 한개의 class에 속한다면
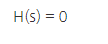
3. positive와 negative 샘플의 개수가 동일할 경우

+ 이진 분류에 대한 Entropy 그래프

< Information Gain(정보 이득) >
attribute(속성)에 따라 샘플들의 집합을 분할할 때, 예상되는 엔트로피(entropy) 감소량의 계산 방식중 하나
집합 S에 대해 attribute(속성) A에 대한 Information gain : G(S,A)

예시 )
=> G(S,A) > 0 : 엔트로피 감소 => 불순도 감소 => class 분류 잘됨 => 성능 향상
=> G(S,A) < 0 : 엔트로피 증가 => 불순도 증가 => class 분류 잘안됨 => 성능 하락
< ID3 Algorithm >
Information gain을 통해 Decision tree learning을 하는 것
예시)

처음 엔트로피
14개의 sample (5 no , 9 yes)

4개의 A(Outlook, Temp, Humidity, Windy)에 대하여, Information Gain 계산



=> Outlook이 가장 Gain이 크다=> 맨처음 Decision node( Root node)로 Outlook 선택

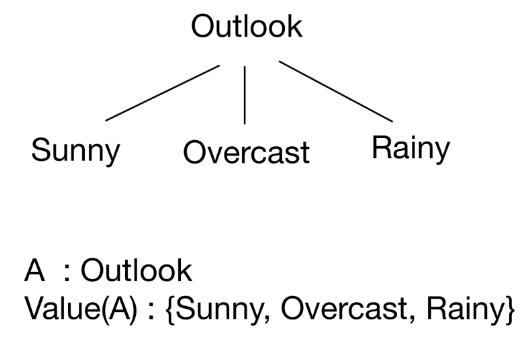
Outlook을 통해 3개의 branch로 나누었음
Overcast는 Yes만 있으므로 끝내고,
나머지 A인 windy와 Humidity의
Value(A) : windy의 경우 {False,True} , Humidity의 경우 {High, Normal}
에 대하여 나눠보니,
play가 Yes와 No로 딱 나눠졌다.
=> 이렇게 class가 딱 나눠질 때 까지 반복해서 가지를 뻗어나간다.
< Gini Impurity(지니 불순도)(=Gini index) >
: 어떤 집합에서 한 항목을 뽑아 무작위로 라벨을 추정할 때 틀릴 확률
CART에 쓰인다.(Classification And Regression Tree)
< CART의 Classification >
Gini Impurity(Gini index)는 다음과 같은 수식을 통해 계산한다.

=> 집합 내에 class의 개수가 적을 수록 Gini impurity 가 작아진다.
=> 분류를 통해 나눠진 집합 내 동일한 샘플들만 있도록 만드는 것이 목표
CART 알고리즘의 classification에서는 분기가 2개로만 나뉜다.
어떤 조건에 대해서 참인가 거짓인가로 나뉜다.
예시)

상위 노드의 지니 불순도를 구하고,
어떤 분류 기준(A)의 가능한 조건들(a)중에서 하나의 조건만 선택하고,
그 조건(a)의 참 or 거짓으로 branch를 나눠서 샘플들을 분류한다.
나뉘어진 두 집합의 지니 불순도를 구하고,
각 집합의 샘플 개수만큼 그 집합의 지니 불순도에 가중치를 둬서 가중합 한다.
이 가중합 지니 불순도(Weighted Gini impurity)가 상위 노드의 지니 불순도보다 작게 만드는 것이 목표이다.
가중합 지니 불순도(Weighted Gini impurity)

많은 분류 기준들(A)과 조건들(a)이 있을텐데,
상위 노드의 지니 불순도와 비교했을 때, 가장 많이 지니 불순도를 줄이는 A의 a를 선택한다.
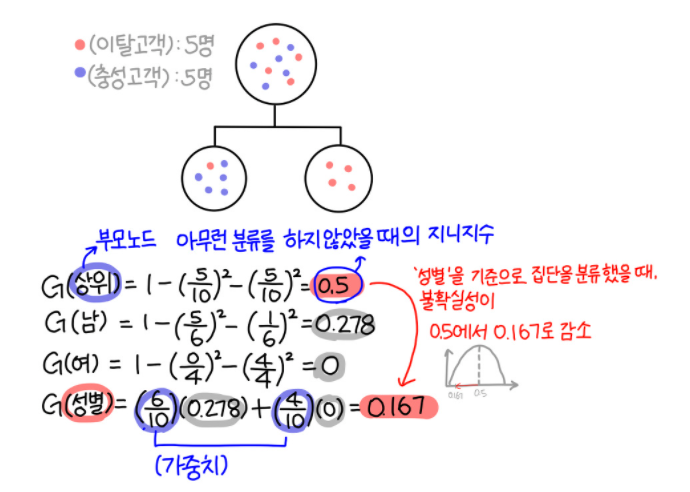
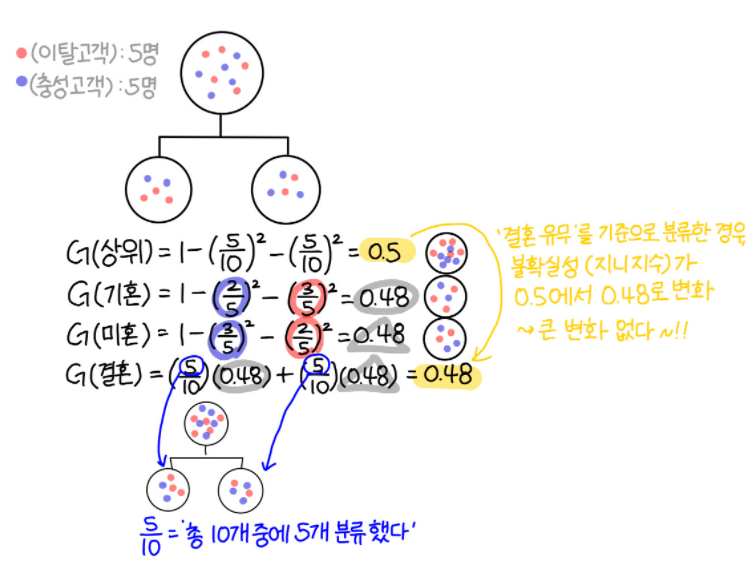
사람(A)의 성별(a)을 고를것인지, 사람(A)의 결혼유무(a)를 고를것인지를 결정하려 하는데,
사람(A)의 성별(a)을 고를경우 지니계수가 더 많이 줄어드니까
=> 사람(A)의 성별(a)를 분류 방식(A,a)로 선택
< CART의 Regression >
CART의 이름에서 Regression Tree가 있다.
회귀는 어떻게 할까?
가중합 지니 불순도(Weighted Gini impurity)

가중합 지니 불순도에서 G대신에 실제값과 예측값의 오차를 이용한다.
즉, MSE(평균제곱오차)나 RSS(잔차 제곱 합)을 사용할 수 있다.

다음과 같은 샘플에 2가지로 나눌 x=a를 구한다.

만약 MSE를 쓸 경우,
각각 해당영역의 sample의 y값과 y평균의 MSE를 구하고,
그 합을 각각 MSEL , MSER 이라고 하자,
그렇다면 이에 대해 Weighted sum을 하면

가 된다.
이 J를 가장 작게 만드는 x=a를 구한다.
그 이후 또 구간을 나눌 선 x=a'을 구한다.

당연히 J를 최소화 해야 한다.
하지만 이 축이 너무 많아지면, 과적합 된다
(축이 많아진다 <=> 트리 가지가 너무 길어진다.)


이런 과적합 문제를 해결하기 위해 max_depth(가지 길이=나누는 구분선 개수)를 지정해 줄 수 있다.
'머신러닝(기계학습)' 카테고리의 다른 글
| 논문을 통해 XGBOOST 완전히 이해하기(Bagging과 Boosting) (0) | 2022.10.10 |
|---|---|
| GBM(Gradient Boost Machine)이란? +학습이 되는 원리 자세히 설명 (0) | 2022.10.10 |